AMS-TeX (verzia 2.0)
Spďż˝	Kapitola 4. Moďż˝nosti ďż˝pravy ďż˝lďż˝nku, ktorďż˝ poskytuje "amsppt.sty".	ďż˝alej

4.2. ďż˝truktďż˝ra samostatnďż˝ho ďż˝lďż˝nku

()\input amstex*	riadok nemusďż˝ byďż˝ uvedenďż˝, pokiaďż˝ uďż˝ mďż˝me sďż˝bor AMSTEX.TEX skompilovanďż˝, t.j. vytvorenďż˝ sďż˝bor AMSTEX.FMT
()\documentstyle{amsppt}*	vďż˝etky veci uvedenďż˝ v tejto kapitole sa tďż˝kajďż˝ prďż˝ve uvedenďż˝ho ďż˝tďż˝lu, je moďż˝nďż˝ vytvďż˝raďż˝ si vlastnďż˝ ďż˝tďż˝ly a do zďż˝tvoriek napďż˝saďż˝ ich nďż˝zov
{preambulovďż˝ veci}	(Pozri odsek nazvanďż˝ Preambulovďż˝ prďż˝kazy a prďż˝kazy na ďż˝pravu celďż˝ho ďż˝lďż˝nku)
\topmatter	(Pozri odsek nazvanďż˝ Hlaviďż˝kovďż˝ prďż˝kazy)
\title ... \\... \endtitle
\author ... \\... \endauthor
\affil ... \\... \endaffil
\address ... \endaddress
\email ... \endemail
\dedicatory ... \enddedicatory
\date ... \enddate
\thanks ... \endthanks
\translator ... \endtranslator
\keywords ... \endkeywords
\subjclass ... \endsubjclass
\abstract ... \endabstract
\toc ... \endtoc
\endtopmatter
(*)\document
{vlastnďż˝ dokument}
\Refs
{zoznam literatďż˝ry }	(Pozri odsek nazvanďż˝ Pďż˝sanie literatďż˝ry)
\endRefs
(*)\enddocument

4.2.1. Prďż˝klad ďż˝tandardnej ďż˝pravy prvej strďż˝nky ďż˝lďż˝nku:

\title Lucid operators on Banach spaces \endtitle
\author Peter Kissel and Eberhard Schock \endauthor
\affil Universit\"at Kaiserlautern\endaffil
\address Universit\"at Kaiserlautern, Mathematik, Postfach 3049, D-6750 Kaiserslautern, Bundesrepublik Deutschland \endaddress
\email  xx\@yy \endemail
\address Universit\"at Kaiserlautern, \dots \endaddress
\email  xx\@yy \endemail
\dedicatory  Dedicated to  \dots \enddedicatory
\date March 18, 1991 \enddate
\thanks    The authors would like to thank Prof.\ J.~R.~Retherford, Baton Rouge, for many stimulating discussions\endthanks
\translator \dots \endtranslator
\keywords  Operator ideals, unconditional convergence\endkeywords
\subjclass Primary 47D30;~Secondary 40A30\endsubjclass
\abstract
We consider an ideal of operators which have a pointwise unconditional
representation and we investigate the relationship between them
and some other operator ideals.\endabstract
\toc
\widestnumber\head{1.1.}
\widestnumber\subhead{1.1.1.}
\specialhead{1} Toto je ``specialhead'' nadpis \page 1\endspecialhead
\head{1.1.} Toto je ``head'' nadpis \page 2\endhead
\subhead{1.1.1} Toto je ``subhead'' nadpis\endsubhead
\subsubhead{} Toto je ``subsubhead'' nadpis \endsubsubhead
\endtoc
\endtopmatter
\document
A tu zaďż˝ďż˝na text ďż˝lďż˝nku \dots
\enddocument

ďż˝oho vďż˝sledkom je:

$\title Lucid operators on Banach spaces \endtitle \author Peter Kissel and Eberhard Schock \endauthor \affil Universit\"at Kaiserlautern\endaffil \address Universit\"at Kaiserlautern, Mathematik, Postfach 3049, D-6750 Kaiserslautern, Bundesrepublik Deutschland \endaddress \email xx\@yy \endemail \address Universit\"at Kaiserlautern, \dots \endaddress \email xx\@yy \endemail \dedicatory Dedicated to \dots \enddedicatory \date March 18, 1991 \enddate \thanks The authors would like to thank Prof.\ J.~R.~Retherford, Baton Rouge, for many stimulating discussions\endthanks %\translator \dots \endtranslator \keywords Operator ideals, unconditional convergence\endkeywords \subjclass Primary 47D30;~Secondary 40A30\endsubjclass \abstract We consider an ideal of operators which have a pointwise unconditional representation and we investigate the relationship between them and some other operator ideals.\endabstract \toc \widestnumber\head{1.1.} \widestnumber\subhead{1.1.1.} \specialhead{1} Toto je ``specialhead'' nadpis \page 1\endspecialhead \head{1.1.} Toto je ``head'' nadpis \page 2\endhead \subhead{1.1.1} Toto je ``subhead'' nadpis\endsubhead \subsubhead{} Toto je ``subsubhead'' nadpis \endsubsubhead \endtoc \endtopmatter \document A tu začína text článku \dots \enddocument$

4.2.2. Hlaviďż˝kovďż˝ prďż˝kazy

Mďż˝ďż˝u byďż˝ uvedenďż˝ v ďż˝ubovoďż˝nom poradďż˝, ďż˝okoďż˝vek je moďż˝nďż˝ vynechaďż˝. Grafickďż˝ ďż˝pravu (typ pďż˝sma, umiestnenie textu, preddefinovanďż˝ pďż˝sanie niektorďż˝ch vecďż˝, napr. slova "Abstract") robďż˝ ďż˝tďż˝l sďż˝m.

Ak chceme zruďż˝iďż˝ preddefinovanie nejakej veci (napr. typ pďż˝sma, vkladanie textu), pouďż˝ijeme \nofrills za prďż˝sluďż˝nďż˝m kďż˝ďż˝ďż˝ovďż˝m slovom. Napr. \abstract \nofrills{\smc Struďż˝nďż˝ obsah.}...\endabstract.
Viacriadkovďż˝ hlaviďż˝ky, ktorďż˝ sďż˝ centrovanďż˝ (\title,\affil,\author, \dedication) sďż˝ tieďż˝ samy rozdeďż˝ovanďż˝ do riadkov, explicitnďż˝ zlom riadku je v tomto prďż˝pade ďż˝pecifikovanďż˝ pomocou \\. Na ostatnďż˝ hlaviďż˝ky sa vzďż˝ahujďż˝ normďż˝lne odstavcovďż˝ prďż˝kazy. V hlaviďż˝kďż˝ch, ktorďż˝ sďż˝ pďż˝sanďż˝ ako poznďż˝mky pod ďż˝iarou (\thanks) musďż˝ byďż˝ koniec odstavca ďż˝pecifikovanďż˝ \endgraf
Okrem \address, \email a \thanks mďż˝ďż˝u byďż˝ ostatnďż˝ hlaviďż˝ky pouďż˝itďż˝ najviac raz.
Kaďż˝dďż˝ \email musďż˝ byďż˝ predchďż˝dzanďż˝ \address.

Okolie \toc a \endtoc poskytuje prostredie na pďż˝sanie obsahov v ďż˝vode ďż˝lďż˝nku. Prďż˝klad pouďż˝itia:

\toc
\widestnumber \head {1.1 }	Pouďż˝ijeme, ak chceme zmeniďż˝ ďż˝ďż˝rku odsadenia \head-nadpisov, preddefinovanďż˝ ďż˝ďż˝rka na ,1.'
\widestnumber \subhead {100.1 }	Pouďż˝ijeme, ak chceme zmeniďż˝ ďż˝ďż˝rku odsadenia \subhead a \subsubhead-nadpisov, preddefinovanďż˝ ďż˝ďż˝rka na ,1.1.'
\specialhead {... }... \page ... \endspecialhead
\head {... }... \page ... \endhead
\subhead {... }... \page ... \endsubhead
\subsubhead {... }... \page ... \endsubsubhead
...	Uvďż˝dzajďż˝ sa nďż˝zvy jednotlivďż˝ch kapitol, ... v poradďż˝, v akom sa vyskytujďż˝ v ďż˝lďż˝nku. Do {... } sa pďż˝ďż˝e ďż˝ďż˝slo kapitoly (pokiaďż˝ ho nechceme niekde uviesďż˝, nutnďż˝ napďż˝saďż˝ {}). Parameter \page je nepovinnďż˝, udďż˝va ďż˝ďż˝slo strany, kde zaďż˝ďż˝na uvedenďż˝ kapitola.
\endtoc

4.2.3. Preambulovďż˝ prďż˝kazy a prďż˝kazy na ďż˝pravu celďż˝ho ďż˝lďż˝nku

V preambulovej ďż˝asti by sa mali uvďż˝dzaďż˝ prďż˝kazy s platnosďż˝ou pre celďż˝ dokument (napr. veďż˝kosďż˝ strďż˝nky, ...).

(*)\pagewidth{vzd} ďż˝pecifikuje ďż˝ďż˝rku textu, (*)\pageheight{vzd} vďż˝ďż˝ku
(*)\hcorrection<vzd>, reps. (*)\vcorrectio<vzd> ďż˝pecifikuje posun obsahu strany k pravďż˝mu, resp. dolnďż˝mu okraju pri tlaďż˝enďż˝ textu.
(*)\pageno=... ďż˝pecifikuje ďż˝ďż˝slo strďż˝nky, od ktorej sa mďż˝ zaďż˝aďż˝ ďż˝ďż˝slovaďż˝; moďż˝no meniďż˝ kdekoďż˝vek v texte (ak zadďż˝me zďż˝pornďż˝ ďż˝ďż˝slo, ďż˝ďż˝sluje rďż˝mskymi.)
\Monograph ak sa jednďż˝ o kapitolu knihy.

ďż˝tandardnďż˝ ďż˝prava strďż˝nky ďż˝lďż˝nku je takďż˝, ďż˝e (okrem prvej strany) zďż˝hlavie strany obsahuje momentďż˝lne ďż˝ďż˝slo strany a navyďż˝e zďż˝hlavie pďż˝rnej (nepďż˝rnej) strany obsahuje poloďż˝ku ďż˝pecifikovanďż˝ \author (\title), stopa je prďż˝zdna. Prvďż˝ strana mďż˝ zďż˝hlavie prďż˝zdne a ďż˝ďż˝slo strany je umiestnenďż˝ centrovane na spodu strany, v pravom dolnom rohu je napďż˝sanďż˝ "Typeset by AmSTeX".

ďż˝pecifikďż˝ciu zďż˝hlavia pďż˝rnej (nepďż˝rnej) strďż˝nky moďż˝no meniďż˝ \leftheadtext{...} (\rightheadtext{...}), najlepďż˝ie hneďż˝ po ďż˝asti \author ...\endauthor (\title...\endtitle). ďż˝ďż˝slo strďż˝nky ostďż˝va v zďż˝hlavďż˝. Zďż˝hlavie je pďż˝sanďż˝ automaticky veďż˝kďż˝mi pďż˝smenami: \rightheadtext\nofrills{...} umoďż˝ďż˝uje zmeniďż˝ toto preddefinovanie. (Analogicky pre \leftheadtext.)
\NoRunningHeads odstraďż˝uje ďż˝plne zďż˝hlavia strďż˝nok, strďż˝nky sďż˝ ďż˝ďż˝slovanďż˝ centrovane na spodu strďż˝nky.
\NoPageNumbers odstraďż˝uje ďż˝ďż˝slovanie strďż˝n.
(*)\headline={...} umoďż˝ďż˝uje ďż˝pecifikovaďż˝ umiestnenďż˝ ďż˝ďż˝slo strďż˝nky v takto definovanom zďż˝hlavďż˝. Prďż˝klad: \headline={\ifodd\pageno{Nepďż˝rna strana} \else{Pďż˝rna strana}\fi}
(*)\footline={...} umoďż˝ďż˝uje ďż˝pecifikovaďż˝ neďż˝tandardnďż˝ stopu strďż˝nky. Pri preddefinovanom ďż˝tďż˝le sa stopa objavďż˝ na strďż˝nke len pri sďż˝ďż˝asnom pouďż˝itďż˝ \NoRunningHeads. (Ak chceme maďż˝ na strďż˝nke zďż˝roveďż˝ stopu i zďż˝hlavie, pri pouďż˝itďż˝ ďż˝tďż˝lu amsppt.sty by sme museli viac vecďż˝ predefinovaďż˝.)
"Typeset by AmSTeX" na spodu prvej strany je umiestďż˝ovanďż˝ ako reklama vďż˝robcu. Odstrďż˝niďż˝ sa dďż˝ priamo v preddefinovanom ďż˝tďż˝le (ďż˝o vďż˝ak nie je moc sluďż˝nďż˝) alebo napďż˝sanďż˝m {\catcode`\@=11\gdef\logo@{}}hneďż˝ za riadkom \documentstyle. (POZOR, na opaďż˝nďż˝ apostrof!!!)

4.2.4. Preddefinovanďż˝ okolia na pďż˝sanie nadpisov kapitol

Existujďż˝ 4 rďż˝zne ďż˝rovne:

\specialhead ... \endspecialhead - neodsadenďż˝ nadpis pďż˝sanďż˝ tuďż˝ne, nasledujďż˝ci text pokraďż˝uje ako novďż˝ odstavec, explicitnďż˝ zlom riadku musďż˝ byďż˝ ďż˝pecifikovanďż˝ \\.
\head ... \endhead - centrovanďż˝ nadpis pďż˝sanďż˝ kapitďż˝lkami, explicitnďż˝ zlom riadku musďż˝ byďż˝ ďż˝pecifikovanďż˝ \\.
\subhead ... \endsubhead - neodsadenďż˝ nadpis pďż˝sanďż˝ tuďż˝ne, automaticky doplnenďż˝ bodka za nadpisom, ďż˝alďż˝ďż˝ text pokraďż˝uje ďż˝alej v riadku. Pre explicitnďż˝ ďż˝pecifikďż˝ciu zlomu riadku platia odstavcovďż˝ prďż˝kazy.
\subsubhead ... \endsubsubhead - nadpis odsadenďż˝ od okraja ako odstavec pďż˝sanďż˝ kurzďż˝vou, automaticky doplnenďż˝ bodka za nadpisom ďż˝alďż˝ďż˝ text pokraďż˝uje ďż˝alej v riadku. Pre explicitnďż˝ ďż˝pecifikďż˝ciu zlomu riadku platia odstavcovďż˝ prďż˝kazy.

Prďż˝klad:

\def\s{$\backslash$}
\specialhead Toto je \s specialhead nadpis \newline
A takto pokraďż˝uje ďż˝alďż˝ďż˝ text.
\head Toto je \s head nadpis \endhead
A takto pokraďż˝uje ďż˝alďż˝ďż˝ text.
\subhead Toto je \s subhead nadpis \endsubhead
A takto pokraďż˝uje ďż˝alďż˝ďż˝ text.
\subsubhead Toto je \s subsubhead nadpis \endsubsubhead
A takto pokraďż˝uje ďż˝alďż˝ďż˝ text.

dďż˝va

$\def\s{$\backslash$} \specialhead Toto je \s specialhead nadpis \newline A takto pokračuje ďalší text. \head Toto je \s head nadpis \endhead A takto pokračuje ďalší text. \subhead Toto je \s subhead nadpis \endsubhead A takto pokračuje ďalší text. \subsubhead Toto je \s subsubhead nadpis \endsubsubhead A takto pokračuje ďalší text.$

4.2.5. Preddefinovanďż˝ okolia na pďż˝sanie viet, dďż˝kazov, ...

Existujďż˝ 4 rďż˝zne okolia, lďż˝ďż˝ia sa veďż˝kosďż˝ou odsadenia od ostatnďż˝ho textu, vďż˝berom pďż˝sma. ďż˝iadna ďż˝asďż˝ nasledovanďż˝ v {...} hneďż˝ po nďż˝zve okolia nie je odsadenďż˝, bodka za touto ďż˝asďż˝ou sa dopďż˝ďż˝a automaticky. Aďż˝ na okolie \proclaim je ostatnďż˝ text pďż˝sanďż˝ romďż˝nskym pďż˝smom.

\proclaim{...}... \endproclaim - ďż˝asďż˝ v {...} je tuďż˝ne, zvyďż˝ok ďż˝ikmďż˝m pďż˝smom.
\definition{...}... \enddefinition - medzerovanie, font na pďż˝sanie {...} rovnakďż˝ ako v \proclaim, zvyďż˝ok ale pďż˝sanďż˝ romďż˝nsky.
\example{...}... \endexample - ďż˝plne rovnakďż˝ ako \definition.
\demo{...}... \enddemo - ďż˝asďż˝ v {...} je pďż˝sanďż˝ kurzďż˝vou.
\remark{...} ... \endremark - ďż˝asďż˝ v {...} je pďż˝sanďż˝ kurzďż˝vou, nepridďż˝va na konci extra medzeru ako \demo.

Prďż˝klad:

\proclaim{1.~Veta} Rovnica $x^n+y^n=z^n$ nemďż˝ pre $n>2$ v obore prirodzenďż˝ch ďż˝ďż˝sel rieďż˝enie. \endproclaim
\demo{Dďż˝kaz} Prenechďż˝vame ďż˝itateďż˝ovi. \enddemo
\definition{2.~Definďż˝cia} ďż˝lďż˝nok nazveme "sluďż˝nďż˝m", ak obsahuje aspoďż˝ jednu definďż˝ciu. \enddefinition
\example{3.~Prďż˝klady} A samozrejme pre zrozumiteďż˝nosďż˝ aj normďż˝lnemu smrteďż˝nďż˝kovi, kaďż˝dďż˝ ďż˝lďż˝nok by mal maďż˝ aj prďż˝klad. \endexample
\remark{4.~Poznďż˝mky} Veďż˝ matematika nie sďż˝ len vety a dďż˝kazy ale aj rďż˝zne poznďż˝mky, komentďż˝re. \endremark

dďż˝va

$\proclaim{1.~Veta} Rovnica $x^n+y^n=z^n$ nemá pre $n>2$ v obore prirodzených čísel riešenie. \endproclaim \demo{Dôkaz} Prenechávame čitateľovi. \enddemo \definition{2.~Definícia} Článok nazveme "slušným", ak obsahuje aspoň jednu definíciu. \enddefinition \example{3.~Príklady} A samozrejme pre zrozumiteľnosť aj normálnemu smrteľníkovi, každý článok by mal mať aj príklad. \endexample \remark{4.~Poznámky} Veď matematika nie sú len vety a dôkazy ale aj rôzne poznámky, komentáre. \endremark$

4.2.6. Ostatnďż˝ uďż˝itoďż˝nďż˝ veci ďż˝tďż˝lu "amsppt.sty"

Citďż˝cie je vhodnďż˝ vypisovaďż˝ v tvare \cite{...}, zďż˝tvorky doplnďż˝ ďż˝tďż˝l sďż˝m. Napr. \cite{K-N, 12} dďż˝va
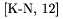
$\cite{K-N, 12}$
Pokiaďż˝ sa chceme v texte odvolďż˝vaďż˝ na tagovanďż˝ (ďż˝ďż˝slovanďż˝) formulky, je vhodnďż˝ pouďż˝iďż˝ (*)\thetag{...}, ktorďż˝ dďż˝va rovnakďż˝ tvar nezďż˝visle na momentďż˝lne nastavenom fonte.
\qed napďż˝ďż˝e na mieste, kde je uvedenďż˝ symbol
$\qed$
(Pouďż˝ďż˝va sa na oznaďż˝enie konca dďż˝kazu.)

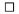
ďż˝truktďż˝ra \block ... \endblock slďż˝ďż˝i pre citovani nejakej vďż˝ďż˝ej ďż˝asti dokumentu. Citovanďż˝ ďż˝asďż˝ je vďż˝razne odsadenďż˝ od ostatnďż˝ho textu.

	Takto predchďż˝dza text.
	\block
	Toto je doslovnďż˝ citďż˝cia pre dlhďż˝ie odstavce, ktorďż˝ zaďż˝ala
	prďż˝kazom \block a bude ukonďż˝enďż˝ prďż˝kazom \endblock
	\endblock
        A takto potom pokraďż˝uje ďż˝alďż˝ďż˝ text.

dďż˝va

$\def\s{$\backslash$} \noindent Takto predchádza text. \block Toto je doslovná citácia pre dlhšie odstavce, ktorá začala príkazom \s block a bude ukončená príkazom \s endblock. \endblock A takto potom pokračuje ďalší text.$

Na vďż˝pis poloďż˝iek slďż˝ďż˝i prostredie \roster\item... \endroster kde jednotlivďż˝ poloďż˝ky sďż˝ ďż˝pecifikovanďż˝ \item a ďż˝ďż˝slovanďż˝ automaticky. Veďż˝kosďż˝ odsadenia poloďż˝iek a ďż˝ďż˝slovania mďż˝ďż˝eme meniďż˝ pomocou \parindent. (Nefunguje \widestnumber\item podďż˝ popisu v [U] !!!) Pokiaďż˝ chceme nejakďż˝ poloďż˝ku oďż˝ďż˝slovaďż˝ inďż˝ďż˝, pouďż˝ďż˝vame ďż˝pecifikďż˝ciu \item ... . Napr.
```
        \parindent1cm
        \roster
          \item Toto je prvďż˝ poloďż˝ka, ďż˝ďż˝slovanďż˝ automaticky.
          \item "\it (i)" Toto je druhďż˝  poloďż˝ka ďż˝ďż˝slovanďż˝ zvlášť.
          \item A toto je tretia poloďż˝ka.
        \endroster
     
```
dďż˝va
$\parindent1cm \roster \item Toto je prvá položka, číslovaná automaticky. \item "\it (i)" Toto je druhá položka číslovaná zvlášť. \item A toto je tretia položka. \endroster$
Ak nie je po \endroster ďż˝pecifikovanďż˝ koniec odstavca, nepokraďż˝uje sa novďż˝m odstavcom. Ak pouďż˝ijeme miesto prvďż˝ho \item \runinitem, text prvej poloďż˝ky bude vďż˝lenenďż˝ normďż˝lne do textu, avďż˝ak ak bude prvďż˝ poloďż˝ka dlhďż˝ia, bude roztiahnutďż˝ na celďż˝ ďż˝ďż˝rku strany. \Runinitem pouďż˝itďż˝ pred odstavcom zarovnďż˝va text dlhďż˝ej prvej poloďż˝ky s ostatnďż˝mi poloďż˝kami.
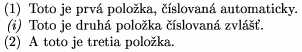
Poznďż˝mky pod ďż˝iarou sa pďż˝ďż˝u pomocou \footnote{...}, teda jednoducho \footnote{V skutoďż˝nosti veďż˝mi jednoducho.}. ďż˝ďż˝slovanďż˝ sďż˝ automaticky.\adjustfootnotemark{ďż˝ďż˝slo} zmenďż˝ďż˝ (zvďż˝ďż˝ďż˝) poradovďż˝ ďż˝ďż˝slo poznďż˝mky o danďż˝ hodnotu. \footnote"..."{...} oznaďż˝uje poznďż˝mku tďż˝m, ďż˝ďż˝m mu predpďż˝ďż˝eme v ďż˝vodzovkďż˝ch. Medzery pred \ sďż˝ ignorovanďż˝.

4.2.7. Pďż˝sanie literatďż˝ry

K pďż˝saniu literatďż˝ry mďż˝ uvedenďż˝ ďż˝tďż˝l preddefinovanďż˝ mnoďż˝stvo kontrolslov. Poloďż˝ky jednotlivej referencie mďż˝ďż˝u byďż˝ uvedenďż˝ v ďż˝ubovoďż˝nom poradďż˝: zmeny pďż˝sma, vkladanie zďż˝tvoriek, ďż˝iarok a celkovďż˝ ďż˝pravu zabezpeďż˝uje ďż˝tďż˝l sďż˝m.

Zoznam literatďż˝ry zaďż˝ďż˝na slovom \Refs (napďż˝ďż˝e centrovane slovo References) a konďż˝ďż˝ s \endRefs.
\widestnumber\no{999}, \widestnumber\key{USA} umoďż˝ďż˝uje meniďż˝ ďż˝ďż˝rku odsadenia literatďż˝ry od jej oznaďż˝enia. Preddefinovanďż˝ hodnota: ďż˝ďż˝rka dvoch ďż˝ďż˝slic.
Medzi \ref a \endref umiestďż˝ujeme poloďż˝ky jednotlivej referencie.
Za \no sa pďż˝ďż˝e ďż˝ďż˝slo referencie (bodka za ďż˝ďż˝slom je doplnenďż˝ automaticky). Ak chceme referenciu oznaďż˝iďż˝ nieďż˝ďż˝m inďż˝m, pouďż˝ijeme \key (vďż˝raz za \key je automaticky umiestnenďż˝ do hranatďż˝ch zďż˝tvoriek).
Za \by sa pďż˝ďż˝e autor. Ak mďż˝me viac referenciďż˝ od jednďż˝ho autora, mďż˝ďż˝eme v ďż˝alďż˝ďż˝ch referenciach namiesto \by pouďż˝iďż˝ \bysame (napďż˝ďż˝e vodorovnďż˝ ďż˝iaru namiesto mena).
Za \paper sa pďż˝ďż˝e nďż˝zov ďż˝lďż˝nku.
Za \inbook sa pďż˝ďż˝e nďż˝zov zbornďż˝ku, v ktorom bol ďż˝lďż˝nok publikovanďż˝.
Za \book sa pďż˝ďż˝e nďż˝zov knihy.
Za \jour sa pďż˝ďż˝e ďż˝asopis.
Za \vol sa pďż˝ďż˝e zvďż˝zok, diel.
Za \yr sa pďż˝ďż˝e rok vydania.
Za \pages sa pďż˝ďż˝u ďż˝ďż˝sla strďż˝nok, pre jednostrďż˝nkovďż˝ ďż˝lďż˝nky mďż˝ďż˝eme pouďż˝iďż˝ \page.
Za \publ sa pďż˝ďż˝e vydavateďż˝.
Za \publaddr sa pďż˝ďż˝e adresa vydavateďż˝a.
Za \eds sa pďż˝ďż˝u menďż˝ editorov (\ed je moďż˝nďż˝ pouďż˝iďż˝ v prďż˝pade 1 editora).
Za \lang sa pďż˝ďż˝e pďż˝vodnďż˝ jazyk, v ktorom ďż˝lďż˝nok vyďż˝iel.
Za \transl sa pďż˝ďż˝e prekladateďż˝.
Za \toappear napďż˝ďż˝e text ,(to appear)'.
Za \issue sa obvykle pďż˝ďż˝e ďż˝ďż˝slo zbornďż˝ku, preddefinovane uvedenďż˝ kontrolslovo pďż˝ďż˝e ,no.'.
Za \paperinfo napďż˝ďż˝eme to, ďż˝o mďż˝ byďż˝ napďż˝sanďż˝ hneďż˝ za nďż˝zvom ďż˝lďż˝nku.
Za \bookinfo napďż˝ďż˝eme to, ďż˝o mďż˝ byďż˝ napďż˝sanďż˝ hneďż˝ za nďż˝zvom knihy.
Za \finalinfo napďż˝ďż˝eme to, ďż˝o mďż˝ byďż˝ napďż˝sanďż˝ na konci referencie. Bodka (prďż˝p. bodkoďż˝iarka, ak pouďż˝ijeme \moreref) za kaďż˝dou referenciou sa dopďż˝ďż˝a automaticky).
\moreref umoďż˝ďż˝uje spojiďż˝ dve referencie do jednej.

Ak chceme potlaďż˝iďż˝ pďż˝sanie interpunkcie medzi niektorďż˝mi poloďż˝kami, pouďż˝ijeme \nofrills. Napr. \finalinfo \nofrills odstraďż˝uje bodku za prďż˝sluďż˝nou referenciou, \nofrills\bookinfo odstraďż˝uje ďż˝iarku pred ďż˝asďż˝ou \bookinfo; \bookinfo\nofrills odstraďż˝uje ďż˝iarku po ďż˝asti \bookinfo. Prďż˝klady:

\Refs
\frenchspacing
\widestnumber\no{9}
\ref\no 4
\by V. I. Arnold, A. N. Varchenko,
 and S. M. Guseuin-Zade
\book Singularities of differentiable maps.~{\rm I}
\publ ``Nauka'' \publaddr Moscow \yr 1982
\lang Russian
\endref
\ref\no 6
\bysame
\book Mathematical problems in the dynamics
 of a viscous incompressible fluid
\bookinfo 2nd rev. aug. ed.
\publ ``Nauka'' \publaddr Moscow \yr 1970
\lang Russian
\transl English transl. of 1st ed.
\book The mathematical theory of viscous
 incompressible flow
\publ Gordon and Breach \publaddr New York
\yr 1963; rev. 1969
\endref
\ref\no 7
\by P. D. Lax and C. D. Levermore
\paper The small dispersion limit for the
 KdV equation.~{\rm I}
\jour Comm. Pure Appl. Math. \vol 36 \yr 1983
\pages 253--290 \nofrills\finalinfo (overview)
\moreref\paper {\rm II}
\jour Comm. Pure Appl. Math.
\vol 36 \yr 1983 \pages 571--594
\moreref\paper {\rm III}
\jour Comm. Pure Appl. Math.
\vol 36 \yr 1983 \pages 809--829 \endref
\widestnumber\key{OSHE}
\ref\key OSHE \by S. Osher
\paper Shock capturing algorithms for equations of mixed type
\inbook Numerical Methods for Partial Differential
 Equations \eds S. I. Hariharan and T. H. Moulton
\publ Longman \publaddr New York \yr 1986
\pages 305--322
\endref
\nonfrenchspacing
\endRefs

Dďż˝va na vďż˝stupe:

$\Refs \frenchspacing \widestnumber\no{9} \ref\no 4 \by V. I. Arnold, A. N. Varchenko, and S. M. Guseuin-Zade \book Singularities of differentiable maps.~{\rm I} \publ ``Nauka'' \publaddr Moscow \yr 1982 \lang Russian \endref \ref\no 6 \bysame \book Mathematical problems in the dynamics of a viscous incompressible fluid \bookinfo 2nd rev. aug. ed. \publ ``Nauka'' \publaddr Moscow \yr 1970 \lang Russian \transl English transl. of 1st ed. \book The mathematical theory of viscous incompressible flow \publ Gordon and Breach \publaddr New York \yr 1963; rev. 1969 \endref \ref\no 7 \by P. D. Lax and C. D. Levermore \paper The small dispersion limit for the KdV equation.~{\rm I} \jour Comm. Pure Appl. Math. \vol 36 \yr 1983 \pages 253--290 \nofrills\finalinfo (overview) \moreref\paper {\rm II} \jour Comm. Pure Appl. Math. \vol 36 \yr 1983 \pages 571--594 \moreref\paper {\rm III} \jour Comm. Pure Appl. Math. \vol 36 \yr 1983 \pages 809--829 \endref \widestnumber\key{OSHE} \ref\key OSHE \by S. Osher \paper Shock capturing algorithms for equations of mixed type \inbook Numerical Methods for Partial Differential Equations \eds S. I. Hariharan and T. H. Moulton \publ Longman \publaddr New York \yr 1986 \pages 305--322 \endref \nonfrenchspacing \endRefs$

4.2.8. ďż˝truktďż˝ra kapitoly v knihe

Pokiaďż˝ pripravujeme knihu, mďż˝ďż˝eme pomocou preddefinovanďż˝ho ďż˝tďż˝lu pďż˝saďż˝ i jednotlivďż˝ kapitoly knihy (nezabudnďż˝ďż˝ na \Monograph pri preambulovďż˝ch prďż˝kazoch), ďż˝ďż˝m budeme maďż˝ zabezpeďż˝enďż˝ jednotnďż˝ ďż˝pravu knihy. Nasledujďż˝ci prďż˝klad ukazuje ďż˝tandardnďż˝ ďż˝pravu kapitoly knihy:

\documenstyle{amsppt}
\Monograph
\topmatter
\title\chapter{4} Matrix Algebras \endtitle
\endtopmatter

ktorďż˝ vyzerďż˝:

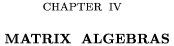
${\catcode`\@=11\gdef\logo@{}} \Monograph \topmatter \title\chapter{4} Matrix Algebras \endtitle \endtopmatter$

Na odstrďż˝nenie slova "CHAPTER" a ostatnďż˝ch preddefinovanďż˝ch vecďż˝ mďż˝ďż˝eme opďż˝ pouďż˝iďż˝ \nofrills, napr. \title\chapter\nofrills{APPENDIX B} The Poisson Integral \endtitle V knihe sa obsah obvykle vytvďż˝ra ako samostatnďż˝ kapitola,kde ďż˝truktďż˝ra \toc ... \endtoc je obsiahnutďż˝ v ďż˝asti \document a \enddocument (nie v ďż˝asti \topmatter ako v ďż˝lďż˝nkoch). Napr.

\documentstyle{amsppt}
\Monograph
\topmatter
\title Contents \endtitle
\endtopmatter
\document
\toc
\title Preface \page{vii} \endtitle
\title Chapter{1} Matrix Algebras \page{1} \endtitle
\head Symmetrical functions \page{1} \endhead
\vdots
\title Bibliography\page 307 \endtitle
\endtoc\newline
\enddocument

V knihe je v zďż˝hlavďż˝ ďż˝avej strany pouďż˝itďż˝ nďż˝zov nasledujďż˝ci po \title, v zďż˝hlavďż˝ pravej strany vďż˝dy aktuďż˝lny text z \head. Pokiaďż˝ uvedenďż˝ nďż˝zvy sďż˝ prďż˝liďż˝ dlhďż˝, pouďż˝ďż˝vame \leftheadtext{} a \rightheadtext{} analogicky ako pri ďż˝lďż˝nkoch. V knihe sa tieďż˝ lďż˝ďż˝i pďż˝sanie preddefinovanďż˝ch okolďż˝: \head je pďż˝sanďż˝ tuďż˝ne (namiesto kapitďż˝lok), okolia \proclaim, \definition, \remark, \demo a \example sďż˝ pďż˝sanďż˝ analogicky ako pri ďż˝lďż˝nkoch, ale sďż˝ navyďż˝e odsadenďż˝ od ďż˝avďż˝ho okraja.

Spďż˝	Obsah	ďż˝alej
Moďż˝nosti ďż˝pravy ďż˝lďż˝nku, ktorďż˝ poskytuje "amsppt.sty".	Hore	"Matematickďż˝" mďż˝d