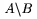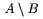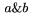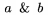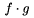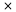AMS-TeX (verzia 2.0)
Spďż˝	Kapitola 5. "Matematickďż˝" mďż˝d	ďż˝alej

5.2. Zďż˝kladnďż˝ pravidlďż˝ pďż˝sania "matematickďż˝ho" textu

V matematickom texte sa ignorujďż˝ vďż˝etky medzery (vrďż˝tane medzery po <Enter>), lebo tie si TeX dorďż˝ba sďż˝m. V rďż˝mci matematickďż˝ho textu sa nesmie objaviďż˝ prďż˝zdny riadok, koniec odstavca sa v rďż˝mci tohto mďż˝du ďż˝pecifikuje odliďż˝ne. ďż˝tandardne sa vďż˝etky pďż˝smenďż˝ pďż˝ďż˝u kurzďż˝vou (odliďż˝nou od textovej kurzďż˝vy), ďż˝ďż˝sla romďż˝nsky.

Vďż˝etky veci uvedenďż˝ v tejto kapitole smďż˝ byďż˝ pouďż˝itďż˝ len v matem. mďż˝de, t.j.musia byďż˝ uvedenďż˝ medzi $...$ alebo $$...$$.

5.2.1. Zďż˝sady sprďż˝vneho pďż˝sania matematickďż˝ho textu

Normďż˝lne znaky majďż˝ veďż˝kosďż˝ nazďż˝vanďż˝ t-size, prvďż˝ exponent s-size, druhďż˝ a ďż˝alďż˝ďż˝ ss-size; ďż˝alej sa uďż˝ veďż˝kosti nezmenďż˝ujďż˝ (TeX zmenďż˝uje tieto veďż˝kosti automaticky). Vďż˝ďż˝ia veďż˝kosďż˝ (vzďż˝ahuje sa len na vďż˝razy) neďż˝ normďż˝lna, je d-size (ktorou sďż˝ ďż˝tandardne pďż˝sanďż˝ centrovanďż˝ formulky). V matematickom mďż˝de sa mďż˝ďż˝eme kedykoďż˝vek prepďż˝naďż˝ medzi tďż˝mito veďż˝kosďż˝ami, kontrolslovami \dsize, \tsize, \ssize a \sssize. Napr. $\sssize xy\ssize xy\tsize xy\dsize xy$ dďż˝va
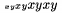
$\sssize xy\ssize xy\tsize xy\dsize xy$
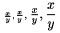
lebo \dsize pďż˝sobďż˝ len vo vďż˝razoch. Ale $\sssize\frac xy,\ssize\frac xy,\tsize\frac xy,\dsize\frac xy$ dďż˝va
$\sssize\frac xy,\ssize\frac xy,\tsize\frac xy,\dsize\frac xy$
\dots pďż˝ďż˝e tri bodky vrďż˝tane sprďż˝vneho medzerovania, napr. $1,\dots ,n$ dďż˝va
$1,\dots ,n$
resp. $1 + ... + n$ dďż˝va
TeX rozliďż˝uje binďż˝rny operďż˝tor a binďż˝rnu relďż˝ciu a podďż˝a toho dopďż˝ďż˝a vhodnďż˝ medzery okolo tďż˝chto symbolov. Pokiaďż˝ chceme, aby symboly tďż˝chto relďż˝ciďż˝ boli chďż˝panďż˝ len ako zďż˝kladnďż˝ znaky, je nutnďż˝ ich daďż˝ do {...}. Napr. $x+y$ dďż˝va
ale $x{+}y$ dďż˝va
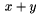
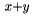
Pretoďż˝e v matematickom mďż˝de mďż˝ ďż˝iarka zvlďż˝tne medzerovanie, mala by byďż˝ gramatickďż˝ ďż˝iarka vďż˝dy mimo tento mďż˝d. Napr. $x,y$ dďż˝va
ale $x$, $y$ dďż˝va
Pozor i pri pďż˝sanďż˝ ďż˝ďż˝sel s desatinnou ďż˝iarkou, napr. $10,0$ dďż˝va
ale $10{,}0$ dďż˝va
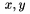
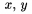
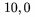
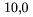
\not dďż˝va "ďż˝krtnutie" binďż˝rneho operďż˝tora, napr. $\not=$ dďż˝va
$\not=$
Ak mďż˝me k dispozďż˝cii fonty s negovanďż˝mi operďż˝ciami, je lepďż˝ie pouďż˝ďż˝vaďż˝ priamo znaky z tďż˝chto fontov (Pozri odsek nazvanďż˝ Negovanďż˝ relďż˝cie v Kapitola 6). V zďż˝kladnej sade fontov sa nachďż˝dza \ne
$(\ne)$
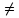
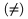
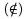
a \notin
$(\notin)$
\underline podtrhďż˝va formulku, napr. $\underline{\underline{4+x}}$ dďż˝va
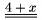
$\underline{\underline{4+x}}$
\overline analogicky "nadtrhďż˝va" formulku, napr. $\overline{\overline{4+x}}$ dďż˝va
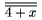
$\overline{\overline{4+x}}$
\boxed umiestďż˝uje formulku do rďż˝mďż˝eka, napr. $\boxed{\boxed{1+1=2}}$ dďż˝va
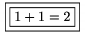
$\boxed{\boxed{1+1=2}}$
Grďż˝cka abeceda je prďż˝stupnďż˝ len v matematickom mďż˝de (Pozri odsek nazvanďż˝ Grďż˝cka abeceda v Kapitola 6)

5.2.2. Pozor na jemnďż˝stky v symboloch

\: zaisďż˝uje sprďż˝vne medzerovanie okolo dvojbodky vo formulkďż˝ch.
\backslash mďż˝ menďż˝ie medzerovanie okolo tohto znaku ako \setminus (pouďż˝ďż˝va sa pre rozdiel mnoďż˝ďż˝n), napr. $A\backslash B$ dďż˝va
$A\backslash B$
ale $A\setminus B$ dďż˝va
$A\setminus B$
\& mďż˝ menďż˝ie medzerovanie okolo tohto znaku ako \and napr.$a\& b$ dďż˝va
$a\& b$
ale $a\and b$ dďż˝va
$a\and b$
\Longrightarrow mďż˝ menďż˝ie medzerovanie okolo tohto znaku ako \implies, napr. $a\Longrightarrow b$ dďż˝va
$a\Longrightarrow b$
ale $a\implies b$ dďż˝va
$a\implies b$
\cdot je symbol pouďż˝ďż˝vajďż˝ci sa pri nďż˝sobenďż˝, napr. $f\cdot g$ dďż˝va
$f\cdot g$
Pokiaďż˝ pouďż˝ijeme pre nďż˝sobenie \*; v prďż˝pade, ďż˝e takďż˝ miesto vyjde na koniec riadku, bude nahradenďż˝
$\times$
inďż˝ďż˝ na tom mieste nebude umiestnenďż˝ ďż˝iadny symbol.

Spďż˝	Obsah	ďż˝alej
"Matematickďż˝" mďż˝d	Hore	TeXovďż˝ matematickďż˝ vďż˝razovďż˝ prostriedky