AMS-TeX (verzia 2.0)
Spďż˝	Kapitola 5. "Matematickďż˝" mďż˝d	ďż˝alej

5.3. TeXovďż˝ matematickďż˝ vďż˝razovďż˝ prostriedky

5.3.1. Exponenty

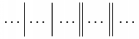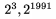
sa pďż˝ďż˝u pomocou ^ alebo \sp. Pokiaďż˝ mďż˝ byďż˝ v exponente viac neďż˝ 1 znak alebo nie zďż˝kladnďż˝ kontrolslovo, je nutnďż˝ exponent uzavrieďż˝ do {}. Napr. $2^3, 2^{1991}$ dďż˝va

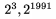
$2^3, 2^{1991}$

Nie je moďż˝nďż˝ pďż˝saďż˝ $2^y^z$, lebo to je moďż˝nďż˝ chďż˝paďż˝ ako

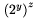
$\left({2^y}\right)^z$

alebo

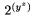
$2^{\left(y^z\right)}$

Preto je nutnďż˝ presne ďż˝pecifikovaďż˝, o ktorďż˝ prďż˝pad sa jednďż˝. Napr. $2^{y^z}$ dďż˝va

$2^{y^z}$

zatiaďż˝ ďż˝o ${2^y}^z$ dďż˝va

${2^y}^z$

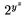
sa pďż˝ďż˝u pomocou _ alebo \sb a platďż˝ pre ne vďż˝etko analogicky ako v predchďż˝dzajďż˝com prďż˝pade. Exponenty a indexy je moďż˝nďż˝ pďż˝saďż˝ v ďż˝ubovoďż˝nom poradďż˝, napr. $2^y_z$ i $2_z^y$ dďż˝va v oboch prďż˝padoch

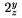
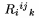
Pokiaďż˝ chceme pďż˝saďż˝ indexy a exponenty tak, aby neboli priamo nad sebou, je nutnďż˝ oddeliďż˝ ich prďż˝zdnou skupinou {}. Napr. $R_i{}^{ij}{}_k$ dďż˝va

$R_i{}^{ij}{}_k$

Pokiaďż˝ chceme pďż˝saďż˝ exponent (index) pred znak, je dobrďż˝ pouďż˝iďż˝ pred ^ (_) prďż˝zdnu skupinu {}.

5.3.3. Operďż˝tory s dolnou a hornou hranicou

Dolnďż˝ i hornďż˝ hranica pre operďż˝tory sa pďż˝ďż˝e analogicky ako indexy a exponenty. Napr. $\sum_{i=1}^{i=10}x_i$ dďż˝va

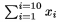
$\sum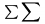_{i=1}^{i=10}x_i$

Hranice je moďż˝nďż˝ pouďż˝ďż˝vaďż˝ s nasledujďż˝cimi operďż˝tormi:

\sum $\sum\dsize\sum$ \prod 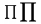$\prod\dsize\prod$ \coprod $\coprod\dsize\coprod$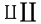
\bigvee 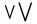$\bigvee\dsize\bigvee$ \bigcap $\bigcap\dsize\bigcap$ \bigodot $\bigodot\dsize\bigodot$
\bigwedge 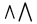$\bigwedge\dsize\bigwedge$ \bigcup $\bigcup\dsize\bigcup$ \bigsqcup $\bigsqcup\dsize\bigsqcup$
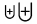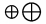\biguplus $\biguplus\dsize\biguplus$ \bigoplus $\bigoplus\dsize\bigoplus$ \bigotimes $\bigotimes\dsize\bigotimes$
integrďż˝lmi
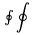\int $\int\dsize\int$ \oint $\oint\dsize\oint$ \iint 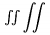$\iint\dsize\iint$
\iiint 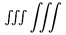$\iiint\dsize\iiint$ \iiiint $\iiiint\dsize\iiiint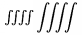$ \idotsint 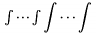$\idotsint\dsize\idotsint$
(\int \int mďż˝ prďż˝liďż˝ veďż˝kďż˝ medzery medzi sebou)
ďż˝tandardnďż˝mi matematickďż˝mi funkciami (Pozri odsek nazvanďż˝ ďż˝tandardnďż˝ matematickďż˝ funkcie)

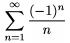
TeX pri formulkďż˝ch pďż˝sanďż˝ch do riadku umiestďż˝uje hranice vpravo od symbolu, pri centrovanďż˝ch formulkďż˝ch (presnejďż˝ie formulkďż˝ch pďż˝sanďż˝ch v d-size, vzďż˝ahuje sa teda i na riadkovďż˝ formulky sďż˝dzanďż˝ v d-size) pod i nad symbol. Vďż˝nimku tvoria integrďż˝ly, kde TeX v riadkovďż˝ch i centrovanďż˝ch formulkďż˝ch umiestďż˝uje hranice vpravo od symbolu. Napr. $\dsize\sum _{n=1}^\infty\frac{(-1)^n}n$ dďż˝va

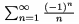
$\dsize\sum_{n=1}^\infty\frac{(-1)^n}n$

ale vynechanďż˝m \dsize dostďż˝vame $\sum_{n=1}^\infty\frac{(-1)^n}n$ , ďż˝o dďż˝va

$\sum_{n=1}^\infty\frac{(-1)^n}n$

\nolimits spďż˝sobuje, ďż˝e tam, kde by sa hranice pďż˝sali normďż˝lne nad i pod symbol, budďż˝ pďż˝sanďż˝ do riadku; \limits naopak spďż˝sobuje, ďż˝e hranice ďż˝tandardne pďż˝sanďż˝ vpravo budďż˝ pďż˝sanďż˝ nad i pod symbol. Napr. $\sum\limits_{n=1}^\infty\frac{(-1)^n}n$ dďż˝va
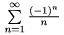
$\sum\limits_{n=1}^\infty\frac{(-1)^n}n$
\NoLimitsOnSums spďż˝sobuje, ďż˝e vo vďż˝etkďż˝ch centrovanďż˝ch formulkďż˝ch sa od napďż˝sania tohto kontrolslova budďż˝ hranice pri sume pďż˝saďż˝ vpravo od tohto symbolu; \LimitsOnSums opďż˝ zapďż˝na normďż˝lnu konvenciu pďż˝sania hranďż˝c pre sumu. Moďż˝no prepďż˝naďż˝ kdekoďż˝vek v texte. \NoLimitsOnInts a \LimitsOnInts funguje analogicky pre integrďż˝ly. Podobne fungujďż˝ tieďż˝ kontrolslovďż˝ \LimitsOnNames a \NoLimitsOnNames pre operďż˝tory definovanďż˝ pomocou \operatornamewithlimits (vrďż˝tane \max,\min, ...).
Pokiaďż˝ niektorďż˝ hranica je viacriadkovďż˝, mďż˝ďż˝eme ju pďż˝saďż˝ nasledovne: medzi \Sb...\\...\endSb umiestďż˝ujeme vďż˝etko, ďż˝o patrďż˝ pod operďż˝tor, jednotlivďż˝ riadky oddeďż˝ujeme pomocou \\; \Sp ...\\...\endSp je analďż˝gia pre hornďż˝ hranicu. Napr. $\sum \Sb 0<j<m\\0<i<n \endSb \Sp k= \infty\\ l= \infty \endSp$ dďż˝va
$\sum \Sb 0<j<m\\0<i<n \endSb \Sp k= \infty\\ l= \infty \endSp$
TeX pridďż˝va zvlďż˝tnu medzeru nad i pod sďż˝ďż˝tacie (integraďż˝nďż˝, ...) hranice. Toto je dďż˝leďż˝itďż˝ uvedomiďż˝ si pri pouďż˝ďż˝vanďż˝ \left a \right. Tomuto pridďż˝vaniu miesta je moďż˝nďż˝ zabrďż˝niďż˝ napďż˝sanďż˝m \shave hneďż˝ za \left. Kontrolslovo \topshave, resp. \botshave zabraďż˝uje pridďż˝vaniu medzery hore, resp. dole. Veďż˝kosďż˝ pridďż˝vanďż˝ho miesta je moďż˝nďż˝ tieďż˝ meniďż˝ pomocou \ChangeBuffer{vzdialenosďż˝} -- tďż˝to hodnota zostane takto nastavenďż˝, pokiaďż˝ ju opďż˝ nepredefinujeme. Kontrolslovo \ResetBuffer nastavďż˝ veďż˝kosďż˝ pridďż˝vanďż˝ho miesta na ďż˝tandardnďż˝ hodnotu. Napr. $\left(\frac{\dsize1+\sum_{i=1}^Na_i}{\dsize1+ \sum_{j=1}^{M}b_j}\right) \qquad \left(\frac{\dsize1+\botshave {\sum_{i=1}^N}a_i}{\dsize1+\topshave{\sum_{j=1} ^{M}b_j}} \right)$ dďż˝va
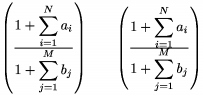
$\left(\frac{\dsize1+\sum_{i=1}^Na_i}{\dsize1+\sum_{j=1}^{M}b_j} \right) \qquad \left(\frac{\dsize1+\botshave{\sum_{i=1}^N}a_i}{\dsize1+ \topshave{\sum_{j=1} ^{M}b_j}}\right)$

5.3.4. Derivďż˝cia

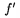
pďż˝ďż˝e sa pomocou ' (ale pozor, len v matematickom mďż˝de) alebo \prime. Pokiaďż˝ chceme pďż˝saďż˝ derivďż˝cie pomocou \prime, sprďż˝vne sa pďż˝ďż˝e $f^\prime$ , ďż˝o dďż˝va

$f^\prime$

Viacnďż˝sobnďż˝ derivďż˝cie mďż˝ďż˝eme pďż˝saďż˝ buďż˝ $f_2"'$ alebo $f_2^{\prime\prime\prime}$ , oboje dďż˝va

Podobne nie je rozdiel, ďż˝i napďż˝ďż˝eme $g^{\prime2}$ , alebo $g'{}^2$ , oboje dďż˝va

$g'{}^2$

5.3.5. Odmocniny

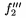
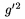
\sqrt{...} je znak pre druhďż˝ odmocninu, pokiaďż˝ sa vzďż˝ahuje len na 1 znak, je moďż˝nďż˝ zďż˝tvorky vynechaďż˝, napr. $\sqrt{a+\sqrt{1+d}+\sqrt z}+\sqrt y$ dďż˝va

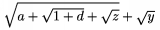
$\sqrt{a+\sqrt{1+d}+\sqrt z}+\sqrt y$

Pokiaďż˝ by sme chceli maďż˝ vďż˝etky znaky odmocnďż˝n rovnakej veďż˝kosti, pouďż˝ijeme \mathstrut ("mathstrut" je neviditeďż˝nďż˝ symbol, ktorďż˝ho vďż˝ďż˝ka je rovnďż˝ maximďż˝lnej vďż˝ďż˝ke pďż˝smen, pri ktorďż˝ch je pouďż˝itďż˝). Napr. $\sqrt a +\sqrt d +\sqrt y+\sqrt {\mathstrut a} +\sqrt{\mathstrut d} +\sqrt{\mathstrut y}.$ dďż˝va
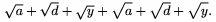
$\sqrt a +\sqrt d +\sqrt y+\sqrt{\mathstrut a} +\sqrt{\mathstrut d} +\sqrt{\mathstrut y}.$
Vyďż˝ďż˝ie odmocniny mďż˝ďż˝eme pďż˝saďż˝ pomocou \root<\uproot{ďż˝ďż˝slo}\leftroot{ďż˝ďż˝slo} ... \of {...}. Kontrolslovďż˝ \uproot (pohyb odmocniteďż˝a vo vertikďż˝lnom smere) a \leftroot (pohyb odmocniteďż˝a v horizontďż˝lnom smere) sďż˝ nepovinnďż˝. Napr. $\root\uproot 3\leftroot{-2}\alpha+\beta \of{1+\frac ab}; \root\alpha+\beta\of{1+\frac ab}$ dďż˝va
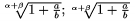
$\root\uproot 3\leftroot{-2}\alpha+\beta\of{1+\frac ab}; \root\alpha+\beta\of{1+\frac ab}$

5.3.6. Kongruencie

\bmod pďż˝ďż˝e len slovo mod a nedodďż˝va zďż˝tvorky okolo; napr. $\gcd(m,n)=\gcd(n,m\bmod n)$ dďż˝va
$\gcd(m,n)=\gcd(n,m\bmod n)$
\pmod pďż˝ďż˝e slovo mod a dodďż˝va okrďż˝hle zďż˝tvorky okolo; napr. $x\equiv y+1\pmod{m^2}$ dďż˝va
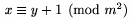
$x\equiv y+1\pmod{m^2}$
\mod rovnakďż˝ ako \pmod, ale nedodďż˝va zďż˝tvorky; napr. $x\equiv y+1\mod{m^2}$ dďż˝va
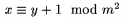
$x\equiv y+1\mod{m^2}$
\pod dodďż˝va samo zďż˝tvorky okolo, ale nepďż˝ďż˝e slovo mod; napr. $x\equiv y+1\pod{m^2}$ dďż˝va
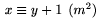
$x\equiv y+1\pod{m^2}$

5.3.7. Zlomky

pďż˝ďż˝u sa pomocou \frac{...}{...}. Ak je ďż˝itateďż˝ alebo menovateďż˝ len 1 znak, je moďż˝nďż˝ zďż˝tvorky vynechaďż˝. TeX automaticky upravuje veďż˝kosďż˝ zlomkov podďż˝a toho, ďż˝i sďż˝ pďż˝sanďż˝ v texte alebo v centrovanďż˝ch formulkďż˝ch. Meniďż˝ tieto veďż˝kosti je moďż˝nďż˝ prepďż˝nanďż˝m "size" (viďż˝ size) (Pozri bliďż˝ďż˝ie) Navyďż˝e \tfrac je skratka za \tsize\frac; \dfrac je skratka za \dsiz\frac.

\thickfrac je zlomok s hrubďż˝ou zlomkovou ďż˝iarou. Napr. \dsize\frac x{y+1};\dsize\thickfrac x{y+1}$ dďż˝va
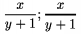
$\dsize\frac x{y+1};\dsize\thickfrac x{y+1}$
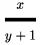
Okrem toho pomocou \thickness{ďż˝ďż˝slo} je moďż˝nďż˝ meniďż˝ hrďż˝bku zlomkovej ďż˝iary, napr. $\dsize\thickfrac\thickness{2.3}x{y+1}$ dďż˝va zlomkovďż˝ ďż˝iaru 2.3 krďż˝t hrubďż˝iu ako pri \thickfrac:
$\dsize\thickfrac\thickness{2.3}x{y+1}$
Ak chceme urobiďż˝ zlomkovďż˝ ďż˝iaru dlhďż˝iu, vsunieme napr. do ďż˝itateďż˝a i menovateďż˝a z obidvoch strďż˝n ďż˝zku medzeru veďż˝kosti \,. Napr. $\frac ab=\dfrac{\,\frac ac\,}{\,\frac bc\,}$ ďż˝ďż˝m dostďż˝vame
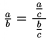
$\frac ab=\dfrac{\,\frac ac\,}{\,\frac bc\,}$
Ak potrebujeme nejakďż˝ zďż˝tvorky okolo zlomku, je vďż˝hodnďż˝ pouďż˝iďż˝ \fracwithdelims<ďż˝av.zďż˝tv.><pr.zďż˝tv.>, napr. $\fracwithdelims(>12$ dďż˝va
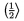
$\fracwithdelims(>12$
V takďż˝chto prďż˝padoch mďż˝ďż˝eme pouďż˝iďż˝ tieďż˝ \left ...\right okolo \frac 12 (Pozri odsek nazvanďż˝ Veďż˝kosti zďż˝tvoriek a oddeďż˝ovaďż˝ov). TeX ale dďż˝va potom odliďż˝nďż˝ medzerovanie. Navyďż˝e \left a \right nemďż˝ďż˝eme pouďż˝iďż˝ v akejkoďż˝vek obecnej konďż˝trukcii. Existuje tieďż˝ \thickfracwithdlims pre zlomky s nami ďż˝pecifikovanou hrďż˝bkou zlomkovej ďż˝iary a zďż˝tvorkami okolo. Napr. $\thickfracwithdelims<>\thickness0nk$ dďż˝va
$\thickfracwithdelims<>\thickness0nk$
Pre reďż˝azovďż˝ zlomky sa pouďż˝ďż˝vajďż˝ konďż˝trukcie, ktorďż˝ sa lďż˝ďż˝ia umiestnenďż˝m vďż˝razov v ďż˝itateli: \cfrac -- centrovanie, \lcfrac -- vďż˝razy vďż˝avo a \rcfraci -- vďż˝razy vpravo; vďż˝razy v menovateli sďż˝ vďż˝dy centrovanďż˝; reďż˝azovďż˝ zlomok ako celok musďż˝ byďż˝ vďż˝dy ukonďż˝enďż˝ s \endcfrac. Napr. $\cfrac 1\\ a_1+\cfrac 2\\ a_2+... +\cfrac n \\ a_n \endcfrac\qquad \lcfrac 1\\ a_1+\lcfrac 2\\ a_2+... +\lcfrac n \\ a_n \endcfrac\qquad \rcfrac 1\\ a_1+\rcfrac 2\\ a_2+... +\rcfrac n \\ a_n \endcfrac$ nďż˝m dďż˝va
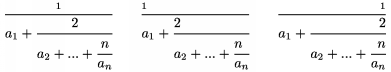
$\cfrac 1\\ a_1+\cfrac 2\\ a_2+... +\cfrac n \\ a_n \endcfrac\qquad \lcfrac 1\\ a_1+\lcfrac 2\\ a_2+... +\lcfrac n \\ a_n \endcfrac\qquad \rcfrac 1\\ a_1+\rcfrac 2\\ a_2+... +\rcfrac n \\ a_n \endcfrac$

5.3.8. Binomickďż˝ koeficienty

\binom{...}{...} pďż˝ďż˝e binomickďż˝ koeficienty, napr. $\binom{i-1}{j+1}$ dďż˝va

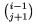
$\binom{i-1}{j+1}$

ďż˝o sa tďż˝ka zmeny veďż˝kostďż˝, \dbinom, \tbinom funguje rovnako ako pri zlomkoch.

5.3.9. Matice

\matrix ... \endmatrix slďż˝ďż˝i k pďż˝saniu matďż˝c (bez zďż˝tvoriek). Jednotlivďż˝ riadky sa oddeďż˝ujďż˝ pomocou \\, jednotlivďż˝ poloďż˝ky v riadku pomocou &. (Pokiaďż˝ by v niektorom riadku bolo menej poloďż˝iek neďż˝ v ostatnďż˝ch riadkoch, riadok je doplnenďż˝ sprava medzerami). Medzi stďż˝pcami je ďż˝tandardnďż˝ vzdialenosďż˝ \quad, stďż˝pce sďż˝ centrovanďż˝. Pokiaďż˝ chceme maticu so zďż˝tvorkami, mďż˝ďż˝eme ju pďż˝saďż˝ pomocou \left i \right, alebo pouďż˝iďż˝ niektorďż˝ preddefinovanďż˝ typy matďż˝c. Napr. $\left( \matrix 1+\beta & 0 & 1-\alpha \\ 1 & 2 & 3-\alpha \\ \alpha & 2 & 3 \endmatrix \right)$ dďż˝va

$\left( \matrix 1+\beta & 0 & 1-\alpha \\ 1 & 2 & 3-\alpha \\ \alpha & 2 & 3 \endmatrix \right)$

\pmatrix ...\endpmatrix je matica ohraniďż˝enďż˝ okrďż˝hlymi
$(\quad)$
zďż˝tvorkami.
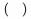
\bmatrix ... \endbmatrix je matica ohraniďż˝enďż˝ hranatďż˝mi
$[\quad]$
zďż˝tvorkami.
\vmatrix ...\endvmatrix je matica ohraniďż˝enďż˝ kolmďż˝mi ďż˝iarami (ako determinant).
$\vert\quad\vert$
\Vmatrix ...\endVmatrix je matica ohraniďż˝enďż˝ dvoma zvislďż˝mi ďż˝iarami (ako norma).
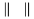
$\Vert\quad\Vert$
Ak chceme zmeniďż˝ ďż˝pravu matice (vzdialenosti medzi stďż˝pcami, centrovanie), je moďż˝nďż˝ zvoliďż˝ si vlastnďż˝ ďż˝pravu matice, pomocou \format. Napr. $\left\{\matrix\format \c &\qquad \c &\qquad \r & \l \\ a+1 & xxxx & 11 & .13 \\ 1 & 8 & & .13 \\ & & 148 & \endmatrix\right\}$ dďż˝va
$\left\{\matrix\format \c &\qquad \c &\qquad \r & \l \\ a+1 & xxxx & 11 & .13 \\ 1 & 8 & & .13 \\ & & 148 & \endmatrix\right\}$
priďż˝om \c znamenďż˝, ďż˝e danďż˝ stďż˝pec bude centrovanďż˝, \r, resp. \l zarovnďż˝vanďż˝ vpravo, resp. vďż˝avo. Vo formďż˝tovacej matici je maximďż˝lny poďż˝et stďż˝pcov urďż˝enďż˝ poďż˝tom & vo formďż˝tovacom riadku. Pokiaďż˝ napďż˝ďż˝eme vo formďż˝tovacom riadku miesto jednďż˝ho znaku \& dva znaky \&\&, potom to, ďż˝o nasleduje, je opakovanďż˝ ďż˝ubovoďż˝nekrďż˝t. Podobne jeden znak \& hneďż˝ za \format znamenďż˝ periodickďż˝ ďż˝truktďż˝ru. Napr.\format \r &&\quad \l \\ znamenďż˝, ďż˝e prvďż˝ stďż˝pec bude zarovnanďż˝ podďż˝a pravďż˝ho kraja a potom ďż˝ubovoďż˝nďż˝ poďż˝et stďż˝pcov podďż˝a ďż˝avďż˝ho kraja, pred ktorďż˝mi predchďż˝dza medzera.
Ak chceme zvďż˝ďż˝iďż˝ vertikďż˝lnu vzdialenosďż˝ medzi riadkami matice, pouďż˝ijeme \spreadmatrixlines{<vzd>} pred \matrix. Vzďż˝ahuje sa na vďż˝etky matice pouďż˝itďż˝ v danom $$...$$. Kdekoďż˝vek za \\ mďż˝ďż˝eme pouďż˝iďż˝ \vspace{<vzd>}, ďż˝o zvďż˝ďż˝ďż˝ vertikďż˝lnu vzdialenosďż˝ medzi riadkami iba na danom mieste.
Ak pďż˝ďż˝eme maticu do textu, veďż˝kosďż˝ matice sa nezmenďż˝uje automaticky. V tomto prďż˝pade je dobrďż˝ pouďż˝iďż˝ \smallmatrix ... \endsmallmatrix. Napr. $\left(\smallmatrix a & b \\ c+1 & d \endsmallmatrix\right)$ dďż˝va
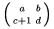
$\left(\smallmatrix a & b \\ c+1 & d\endsmallmatrix\right)$
V tďż˝chto maticiach moďż˝no pouďż˝ďż˝vaďż˝ \format i \vspace, ale nie \spreadmatrixlines.
\hdots, \vdots, \ddots sďż˝ po rade vodorovnďż˝, zvislďż˝ a diagonďż˝lne bodky pre bodkovanie v maticiach, nepresahujďż˝ce prďż˝sluďż˝nďż˝ hranice stďż˝pca alebo riadku. Ak chceme ďż˝pecifikovaďż˝ horizontďż˝lne bodky presahujďż˝ce cez stďż˝pce, mďż˝ďż˝eme pouďż˝iďż˝ \hdotsfor<poďż˝et stďż˝pcov> pre bodky zaďż˝ďż˝najďż˝ce v prvom stďż˝pci a \innerhdotsfor<poďż˝et stďż˝pcov> \after ... pre bodky zaďż˝ďż˝najďż˝ce v ďż˝ubovoďż˝nom inom stďż˝pci, kde namiesto ... sa udďż˝va vzdialenosďż˝ zaďż˝iatku bodiek od predchďż˝dzajďż˝ceho stďż˝pca. Napr. $\pmatrix a_1 & a_2 & \hdots & a_n \\ b_1 & b_2 & \hdots & b_n \\ \vdots & \vdots & \ddots & \vdots \\ d_1 & d_2 & \hdots & d_n \endpmatrix \qquad \pmatrix a_1 & a_2 & \hdots & a_n \\ b_1 & b_2 & \hdots & b_n \\ \hdotsfor 3& 2 \\ d_1 & \innerhdotsfor 2\after\quad & d_n \endpmatrix \qquad$ dďż˝va
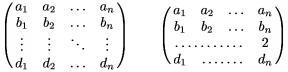
$\pmatrix a_1 & a_2 & \hdots & a_n \\ b_1 & b_2 & \hdots & b_n \\ \vdots & \vdots & \ddots & \vdots \\ d_1 & d_2 & \hdots & d_n \endpmatrix \qquad \pmatrix a_1 & a_2 & \hdots & a_n \\ b_1 & b_2 & \hdots & b_n \\ \hdotsfor 3& 2 \\ d_1 & \innerhdotsfor 2\after\quad & d_n \endpmatrix \qquad$
Je moďż˝nosďż˝ tieďż˝ meniďż˝ medzery medzi bodkami. Namiesto \hdotsfor mďż˝ďż˝eme pouďż˝iďż˝ \spacedots<vzd> \for ... kde vzdialenosďż˝ udďż˝va veďż˝kosďż˝ medzery medzi bodkami; udďż˝va sa bez jednotiek a rozumejďż˝ sa ďż˝tandardnďż˝ jednotky pt. Pre \hdotsfor je to 1.5pt. Analogicky mďż˝ďż˝eme pouďż˝iďż˝ \spaceinnerhdots<vzd> \for... \after... namiesto \innerhdots ... .

5.3.10. Vektory a ďż˝ďż˝pky pďż˝sanďż˝ nad a pod znaky

Vektory sa pďż˝ďż˝u pomocou \overrightarrow (alebo skrďż˝tene \overarrow), napr. \overarrow{x+y} dďż˝va

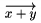
$\overarrow{x+y}$

Okrem toho je moďż˝nďż˝ pouďż˝ďż˝vaďż˝ nasledujďż˝ce "vektorovďż˝" symboly:

\overrightarrow{x+y} alebo tieďż˝\overarrow	$\overarrow{x+y}$
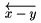\overleftarrow{x-y}	$\overleftarrow{x-y}$
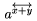a^{\overleftrightarrow{x+y}}	$a^{\overleftrightarrow{x+y}}$
\overline{x+y}	$\overline{x+y}$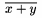
\underrightarrow{x-y} alebo tieďż˝ \underarrow	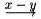$\underarrow{x-y}$
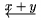\underleftarrow{x+y}	$\underleftarrow{x+y}$
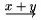\underrightarrow{x+y}	$\underrightarrow{x+y}$
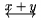\underleftrightarrow{x+y}	$\underleftrightarrow{x+y}$
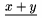\underline{x+y}	$\underline{x+y}$

5.3.11. ďż˝ďż˝pky a znaky pďż˝sanďż˝ nad a pod ďż˝ďż˝pky

ďż˝ďż˝pka sa najjednoduchďż˝ie pďż˝ďż˝e pomocou \to, napr. $f\:X \to Y$ dďż˝va
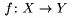
$f\:X \to Y$
Zoznam ostatnďż˝ch ďż˝ďż˝piek je uvedenďż˝ v prďż˝lohe (Pozri odsek nazvanďż˝ ďż˝ďż˝pky v Kapitola 6).
Zo zďż˝kladnďż˝ch ďż˝ďż˝piek sďż˝ navyďż˝e poskladanďż˝ ďż˝ďż˝pky, \dashrightarrow (alebo len \dasharrow), ďż˝o odpovedďż˝
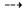
$\dasharrow$
a \dashleftarrow odpovedajďż˝ce
$\dashleftarrow$
ktorďż˝ nie sďż˝ zďż˝kladnďż˝mi znakmi fontov.
Ak chceme nad ďż˝i pod jednoduchďż˝ ďż˝ďż˝pku
nieďż˝o umiestďż˝ovaďż˝, je lepďż˝ie pouďż˝iďż˝ @>>>, resp.@<<<. To, ďż˝o je medzi prvďż˝m a druhďż˝m, resp.druhďż˝m a tretďż˝m znakom < alebo >, sa pďż˝ďż˝e nad ďż˝i pod ďż˝ďż˝pku. Dďż˝ka ďż˝ďż˝pky sa zvďż˝ďż˝uje automaticky. Ak by sme do vďż˝razu nad, ďż˝i pod ďż˝ďż˝pku potrebovali umiestniďż˝ < alebo >, je nutnďż˝ daďż˝ celďż˝ vďż˝raz do zloďż˝enďż˝ch zďż˝tvoriek. Napr. $x @>>{3<4}>$ dďż˝va
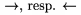
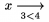
Konďż˝trukcia \underset ... \to{...} umiestďż˝uje to, ďż˝o je za \underset, centrovane pod vďż˝raz, ktorďż˝ nasleduje za \to. Podobne je moďż˝nďż˝ pouďż˝iďż˝ tieďż˝ \overset ... \to{...}. Toto nie je moďż˝nďż˝ pouďż˝iďż˝ k umiestďż˝ovaniu vďż˝razov pod i nad ďż˝ďż˝pku vytvorenďż˝ s \to. Ak umiestďż˝ujeme nieďż˝o nad, ďż˝i pod binďż˝rny operďż˝tor, bude sa to opďż˝ sprďż˝vaďż˝ ako binďż˝rny operďż˝tor (medzerovanie), ale vďż˝razy nad, ďż˝i pod by nemali byďż˝ prďż˝liďż˝ dlhďż˝. Napr. $\overset\text{def}\to =$, resp. $\overset h\to{\underset A\to d}$ dďż˝va
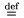
$\overset\text{def}\to =$

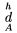
$\overset h\to{\underset A\to d}$
\oversetbrace... \to{...} je analogickďż˝ ako predchďż˝dzajďż˝ce, navyďż˝e so svorkovďż˝mi zďż˝tvorkami, podobne \undersetbrace ... \to{...} Napr. $\oversetbrace\text{$k$ times}\to{x +...+ x} \text{, resp.} \undersetbrace >\,0\to{x+y+z}$ dďż˝va
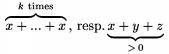
$\oversetbrace\text{$k$ times}\to{x +...+ x}\text{, resp.} \undersetbrace >\,0\to{x+y+z}$
Vodorovnďż˝ svorky je tieďż˝ moďż˝nďż˝ dosiahnuďż˝ pomocou \overbrace a \underbrace a prďż˝padnďż˝ text sa pďż˝ďż˝e analogicky ako pri operďż˝toroch s hranicami. Napr. $\overbrace{x+y+z}^{k\text{-times}}_{<5}$ napďż˝ďż˝e
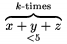
$\overbrace{x+y+z}^{k\text{-times}}_{<5}$

5.3.12. Komutatďż˝vne diagramy

Komutatďż˝vne diagramy sa vytvďż˝rajďż˝ pomocou \CD a \endCD. Medzi tďż˝mito symbolmi sa vytvďż˝rajďż˝ horizontďż˝lne ďż˝ďż˝pky spďż˝sobom popďż˝sanďż˝m v predchďż˝dzajďż˝cej ďż˝asti. Vertikďż˝lne ďż˝ďż˝pky sa vytvďż˝rajďż˝ analogicky, ale pouďż˝ďż˝vajďż˝ sa znaky @VVV pre ďż˝ďż˝pky dole a @AAA pre ďż˝ďż˝pky hore. Symbol \\ sa pouďż˝ďż˝va k oddeďż˝ovaniu riadkov, alebo k vloďż˝eniu prďż˝zdneho riadku. Napr. $\CD G@>\alpha>> H\\ @VfVV @AAgA \\G'@<<\beta< H'\endCD$ dďż˝va

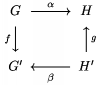
$\CD G@>\alpha>> H\\ @VfVV @AAgA \\G'@<<\beta< H'\endCD$

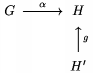
V rohoch, kde neuvďż˝dzame ďż˝iadny vďż˝raz, pďż˝ďż˝eme buďż˝ {}alebo niďż˝. Na miestach, kde majďż˝ byďż˝ vynechanďż˝ ďż˝ďż˝pky, pďż˝ďż˝eme @. . Napr. $\CD G @>\alpha>> H \\@. @AAgA \\@. H'\endCD$ dďż˝va

$\CD G @>\alpha>> H \\@. @AAgA \\@. H'\endCD$

Je moďż˝nďż˝ tieďż˝ pouďż˝iďż˝ @=, resp. @| pre dlhďż˝ vodorovnďż˝, resp. zvislďż˝ znamienko =.
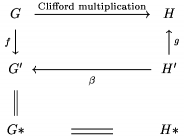
\minCDarrowwidth<vzd>uvedenďż˝ pred diagramom (vo vnďż˝tri $$...$$) zmenďż˝ dďż˝ky ďż˝ďż˝piek v diagrame na uvedenďż˝ rozmer; dlhďż˝ie budďż˝ len v prďż˝pade, ďż˝e text uvedenďż˝ nad ďż˝i pod nimi bude dlhďż˝ďż˝ neďż˝ uvedenďż˝ rozmer. V tomto prďż˝pade vďż˝ak nebudďż˝ vďż˝etky ďż˝ďż˝pky v prďż˝sluďż˝nom stďż˝pci upravenďż˝ na rovnakďż˝ dďż˝ku: \pretend ...\haswidth ... umoďż˝ďż˝uje nastaviďż˝ dďż˝ku ďż˝ďż˝pky podďż˝a dďż˝ky textu. Napr. $\define \bottomarrow{@<<\pretend\beta \haswidth{ \text{ Clifford multiplication}}<} \CD G @>\text{Clifford multiplication}>>H \\ @VfVV @AAgA \\G'\bottomarrow H'\\@|@.\\ G*@=H*\endCD dďż˝va
$\define \bottomarrow{@<<\pretend\beta \haswidth{ \text{ Clifford multiplication}}<} \CD G @>\text{Clifford multiplication}>>H \\ @VfVV @AAgA \\G'\bottomarrow H'\\@|@.\\ G*@=H*\endCD$

Komutatďż˝vne diagramy so ďż˝ikmďż˝mi ďż˝iarami sa v AmSTeXu jednoducho pďż˝saďż˝ nedajďż˝.

5.3.13. Veďż˝kosti zďż˝tvoriek a oddeďż˝ovaďż˝ov

Ak chceme, aby TeX dosadil sprďż˝vnu veďż˝kosďż˝ zďż˝tvoriek okolo vďż˝razu, pouďż˝ijeme \left a \right s presnďż˝m udanďż˝m druhu zďż˝tvoriek. Napr. $\left( \dfrac xy\right]$ dďż˝va

$\left( \dfrac xy\right]$

Uvedenďż˝ sa vzďż˝ahuje na nasledujďż˝ce typy zďż˝tvoriek a oddeďż˝ovaďż˝ov:

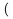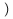	(		)	$\}$	}, \rbrace
$\{$	{, \lbrace	$\vert$	\|, \vert	$\Vert$	\|, \Vert
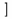$\rbrack$	], \rbrack	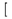$\lbrack$	[, \lbrack	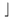$\rfloor$	\rfloor
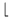$\lfloor$	\lfloor	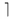$\rceil$	\rceil	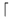$\lceil$	\lceil
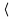$\langle$	\langle	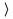$\rangle$	\rangle
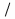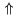	/	$\backslash$	\backslash	$\uparrow$	\uparrow
$\Uparrow$	\Uparrow	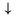$\downarrow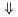$	\downarrow	$\Downarrow$	\Downarrow
$\updownarrow$	\updownarrow	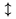$\Updownarrow$	\Updownarrow

\left i \right sďż˝ pďż˝rovďż˝, preto ak nechceme jednu zo zďż˝tvoriek uviesďż˝, treba uviesďż˝ bodku namiesto tejto zďż˝tvorky. Napr. $\left\{ \dfrac xy \right.$ dďż˝va
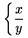
$\left\{ \dfrac xy \right.$
Podďż˝a \left i \right sa urďż˝uje i medzerovanie okolo. Pretoďż˝e znaky [ a ] berie TeX ako znaky nie ako zďż˝tvorky, kvďż˝li sprďż˝vnemu medzerovaniu je nutnďż˝ tieto znaky pďż˝saďż˝ s \left i \right i v zďż˝kladnej veďż˝kosti. Analogicky i pri
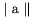
$\vert$ a $\Vert$
ak ich pouďż˝ďż˝vame v zmysle zďż˝tvoriek.
Zvďż˝ďż˝ovanie pomocou \left i \right poskytuje ďż˝ubovoďż˝ne veďż˝kďż˝ symboly.
\left <je skratka za \left \langle, \right>je skratka za \right\rangle.
Niekedy sa ovďż˝em stane, ďż˝e zďż˝tvorka (oddeďż˝ovaďż˝), ktorďż˝ TeX sďż˝m vyberie je vďż˝ďż˝ia (menďż˝ia), ako by sme my chceli. V tom prďż˝pade mďż˝me moďż˝nosďż˝ explicitne ďż˝pecifikovaďż˝ veďż˝kosďż˝ zďż˝tvorky (oddeďż˝ovaďż˝a) v preddefinovanďż˝ch veďż˝kostiach: \big, \Big (asi 1,5 krďż˝t vďż˝ďż˝ie ako \big), \bigg a \Bigg (asi 2,5 krďż˝t vďż˝ďż˝ie ako \bigg). Napr. $\left(\sum^k_{i=1}x_i\right), \biggl(\sum^k_{i=1}x_i\biggr)$ dďż˝va
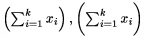
$\left(\sum^k_{i=1}x_i\right), \biggl(\sum^k_{i=1}x_i\biggr)$
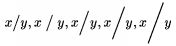
Kvďż˝li sprďż˝vnemu medzerovaniu je dobrďż˝ ďż˝pecifikovaďż˝ otvďż˝racie zďż˝tvorky s koncovkou l a zatvďż˝racie s koncovkou r (nemusia uďż˝ byďż˝ pďż˝rovďż˝). Ak chceme dosiahnuďż˝ medzery ako okolo binďż˝rneho operďż˝tora, pridďż˝va sa koncovka m. Pokiaďż˝ neuvedieme ďż˝iadnu koncovku, medzerovanie okolo je rovnakďż˝ ako okolo kaďż˝dďż˝ho zďż˝kladnďż˝ho symbolu. Napr. $x \big/y , x\bigm/y, x\Big/y, x \bigg/y,x\Bigg/y$ dďż˝va
$x \big/y , x\bigm/y, x\Big/y, x \bigg/y,x\Bigg/y$
Uvedenďż˝ sa vzďż˝ahuje aj na nasledujďż˝ce ďż˝peciďż˝lne oddeďż˝ovaďż˝e, ktorďż˝ sa pouďż˝ďż˝vajďż˝ len s \left ...\right alebo s udanďż˝m presnej veďż˝kosti pomocou \big, ....
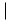$\big\arrowvert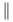$ \big\arrowvert 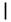$\big\Arrowvert$ \big\Arrowvert $\big\bracevert$ \big\bracevert
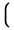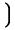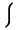$\Big\lgroup$ \Big\lgroup $\Big\rgroup$ \Big\rgroup $\big\lmoustache$ \big\s lmoustache
$\big\rmoustache$ \big\rmoustache
\arrowvert a \Arrowvert na rozdiel od \vert a \Vert majďż˝ rozdielne medzery medzi ďż˝iarami, inďż˝ hrďż˝bku ďż˝iar a inďż˝ medzerovanie okolo. Kontrolslovďż˝ \lgroup a \rgroup je moďż˝nďż˝ pouďż˝iďż˝ len vo veďż˝kostiach \Big a vďż˝ďż˝ďż˝ch. Napr. $\dots \bigg\vert \dots \bigg\arrowvert \dots \bigg \Vert \dots \bigg \Arrowvert \dots$ dďż˝va
$\dots \bigg\vert \dots \bigg\arrowvert \dots \bigg \Vert \dots \bigg \Arrowvert \dots$

Spďż˝	Obsah	ďż˝alej
Zďż˝kladnďż˝ pravidlďż˝ pďż˝sania "matematickďż˝ho" textu	Hore	Texty a fonty v matematickom mďż˝de

\sum	$\sum\dsize\sum$	\prod	$\prod\dsize\prod$	\coprod	$\coprod\dsize\coprod$
\bigvee	$\bigvee\dsize\bigvee$	\bigcap	$\bigcap\dsize\bigcap$	\bigodot	$\bigodot\dsize\bigodot$
\bigwedge	$\bigwedge\dsize\bigwedge$	\bigcup	$\bigcup\dsize\bigcup$	\bigsqcup	$\bigsqcup\dsize\bigsqcup$
\biguplus	$\biguplus\dsize\biguplus$	\bigoplus	$\bigoplus\dsize\bigoplus$	\bigotimes	$\bigotimes\dsize\bigotimes$

\int	$\int\dsize\int$	\oint	$\oint\dsize\oint$	\iint	$\iint\dsize\iint$
\iiint	$\iiint\dsize\iiint$	\iiiint	$\iiiint\dsize\iiiint$	\idotsint	$\idotsint\dsize\idotsint$

$\big\arrowvert$	\big\arrowvert	$\big\Arrowvert$	\big\Arrowvert	$\big\bracevert$	\big\bracevert
$\Big\lgroup$	\Big\lgroup	$\Big\rgroup$	\Big\rgroup	$\big\lmoustache$	\big\s lmoustache
$\big\rmoustache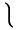$	\big\rmoustache