AMS-TeX (verzia 2.0)
Spďż˝	Kapitola 5. "Matematickďż˝" mďż˝d	ďż˝alej

5.4. Texty a fonty v matematickom mďż˝de

5.4.1. Vkladanie textu

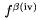
\text{...} umoďż˝ďż˝uje napďż˝saďż˝ jednoriadkovďż˝ text i vo vnďż˝tri matematickďż˝ho mďż˝du fontom aktuďż˝lnym pred vstupom do neho. Medzerovanie okolo je rovnakďż˝, ako by celďż˝ vďż˝raz bol jeden znak matematickďż˝ho mďż˝du. Vo vnďż˝tri \text{...} mďż˝ďż˝eme prepďż˝naďż˝ fonty, i opďż˝ sa prepnďż˝ďż˝ do matematickďż˝ho mďż˝du. Pokiaďż˝ sa pouďż˝ije \text v exponentoch alebo indexoch, automaticky sa menďż˝ jeho veďż˝kosďż˝ (toto neplatďż˝, pokiaďż˝ by sa v \text pouďż˝ilo ďż˝ikmďż˝ pďż˝smo). Napr. $f^{\text{$\beta$(iv)}}$ napďż˝ďż˝e

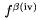
$f^{\text{$\beta$(iv)}}$

\foldedtext sa pouďż˝ďż˝va ako \text, ale umoďż˝ďż˝uje text rozdeliďż˝ do viacerďż˝ch riadkov. Ak chceme presne ďż˝pecifikovaďż˝ ďż˝ďż˝rku textu, pďż˝ďż˝eme \foldedtext \foldedwidth{vzd}{...}. Ak text obsahuje viac odstavcov, \endgraf pouďż˝ďż˝vame na ukonďż˝enie odstavca. Kontrolslovo \topfoldedtext, resp. \botfoldedtext znamenďż˝, ďż˝e zďż˝kladďż˝a celďż˝ho textu je totoďż˝nďż˝ so zďż˝kladďż˝ou hornďż˝ho, resp. dolnďż˝ho riadku textu.Napr. $\topfoldedtext\foldedwidth{30mm} {Toto je text zarovnanďż˝ s hornďż˝m riadkom.} \,\,\, x=1\, \foldedtext\foldedwidth{30mm}{Toto je text nezarovnanďż˝ so ďż˝iadnym riadkom.} \,\,\, x=1\, \botfoldedtext \foldedwidth{30mm} {Toto je text zarovnanďż˝ so spodnďż˝m riadkom.}$ dďż˝va
$\topfoldedtext\foldedwidth{30mm} {Toto je text zarovnaný s horným \newline riadkom.} \,\,\, x=1\, \foldedtext\foldedwidth{30mm}{Toto je text ne\-za\-rov\-na\-ný so žiadnym riad\-kom.} \,\,\, x=1\, \botfoldedtext \foldedwidth{30mm} {Toto je text zarovnaný so spodným \newline riadkom.}$
\intertext{...} umoďż˝ďż˝uje pďż˝saďż˝ text do samostatnďż˝ho riadku medzi viac matematickďż˝ch formuliek pďż˝sanďż˝ch pod sebou v rďż˝mci $$...$$ okolia. (Pozri odsek nazvanďż˝ ďż˝ďż˝slovanie a ďż˝prava centrovanďż˝ch formuliek)

5.4.2. ďż˝tandardnďż˝ matematickďż˝ funkcie

Ak chceme v matematickom mďż˝de napďż˝saďż˝ napr. sin 3x, sprďż˝vnejďż˝ie je nepďż˝saďż˝ "sin" kurzďż˝vou v matematickom mďż˝de, ale normďż˝lnym romďż˝nskym pďż˝smom. Lepďż˝ie neďż˝ $\text {sin $3x $}$ je pouďż˝iďż˝ preddefinovanďż˝ ďż˝tandardnďż˝ funkcie (v predchďż˝dzajďż˝com prďż˝pade \sin), ktorďż˝ dďż˝vajďż˝ sprďż˝vne medzerovanie okolo. Niektorďż˝ z nich, napr. \max, \lim umoďż˝ďż˝ujďż˝ aj umiestďż˝ovanie dolnej a hornej hranice pod a nad danďż˝ symbol. Prehďż˝ad definovanďż˝ch matematickďż˝ch funkciďż˝:

\arccos	\cot	\exp	*\lim	\sec	\cosh
\arcsin	\coth	*\gcd	\ln	\sin	\dim
\arctan	\csc	\hom	\log	\sinh	\lg
\arg	\deg	*\inf	*\max	*\sup	*\Pr
\cos	*\det	\ker	*\min	\tan	\tanh

(* znamenďż˝, ďż˝e u danďż˝ch funkciďż˝ mďż˝ďż˝eme umiestďż˝ovaďż˝ hranice nad i pod danďż˝ funkciu a pouďż˝ďż˝vaďż˝ teda \limits a \nolimits) (Pozri bliďż˝ďż˝ie) Pri predchďż˝dzajďż˝cich funkciďż˝ch nďż˝zov funkcie odpovedďż˝ presne prďż˝sluďż˝nďż˝mu kontrolslovu. Okrem toho sďż˝ preddefinovanďż˝ eďż˝te nasledujďż˝ce funkcie:

*\liminf	$\liminf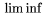$	*\limsup	$\limsup$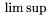
*\injlim	$\injlim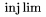$	*\projlim	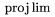$\projlim$
*\varliminf	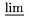$\varliminf$	*\varlimsup	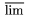$\varlimsup$
*\varinjlim	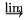$\varinjlim$	*\varprojlim	$\varprojlim$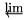

Navyďż˝e mďż˝me moďż˝nosďż˝ definovaďż˝ si vlastnďż˝ operďż˝tory: \operatorname{tg} znamenďż˝, ďż˝e tg (v matem. mďż˝de) sa napďż˝ďż˝e so sprďż˝vnym medzerovanďż˝m a romďż˝nskym typom pďż˝sma, ako by to bol niektorďż˝ z definovanďż˝ch operďż˝torov. So znakmi `'* _ / - -- --- pouďż˝itďż˝mi v definďż˝cii operďż˝tora sa zaobchďż˝dza rovnako ako v normďż˝lnom texte. \operatornamewithlimits{tg} znamenďż˝, ďż˝e tg sa chovďż˝ rovnako ako v predchďż˝dzajďż˝com prďż˝pade, ale je moďż˝nďż˝ naviac pouďż˝iďż˝ \limits a \nolimits (Pozri bliďż˝ďż˝ie).

5.4.3. Bodky ...

\ldots (\cdots) dďż˝va

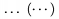
$$\ldots$ ($\cdots$)$

Okrem toho mďż˝ďż˝eme eďż˝te pouďż˝ďż˝vaďż˝ \dots, ktorďż˝ v zďż˝vislosti od situďż˝cie interne volďż˝ jedno z nasledujďż˝cich kontrolslov:

\dotsc -- bodky pred ďż˝iarkou alebo bodkoďż˝iarkou,

\dotsb -- bodky medzi binďż˝rnymi operďż˝tormi alebo relďż˝ciami,

\dotsi -- bodky medzi integrďż˝lmi a \dotso

v ostatnďż˝ch prďż˝padoch. Je zrejmďż˝, ďż˝e pre TeX je niekedy obtiaďż˝ne sprďż˝vne sa rozhodnďż˝ďż˝ a vybraďż˝ vhodnďż˝ bodky pre \dots. Problematickďż˝ bďż˝va koniec formule, kde TeX automaticky dosadzuje \dotso, ďż˝o nemusďż˝ byďż˝ vďż˝dy sprďż˝vne. Preto v takďż˝chto prďż˝padoch je vďż˝dy lepďż˝ia priama ďż˝pecifikďż˝cia niektorej zo spomďż˝nanďż˝ch moďż˝nostďż˝. Ak pouďż˝ijeme na zaďż˝iatku ďż˝i konci definďż˝cie kontrolslovďż˝ \DOTSI alebo \DOTSB, potom pri pouďż˝itďż˝ bodiek "okolo" volania definďż˝cie sa dosadia odpovedajďż˝ce bodky (\dotsi alebo \dotsb), inďż˝ďż˝ by sa dosadilo \dotso. \DOTSX uvedenďż˝ na zaďż˝iatku ďż˝i konci definďż˝cie znamenďż˝, ďż˝e pri pouďż˝itďż˝ bodiek "okolo" volania definďż˝cie sa bude vkladaďż˝ medzera (Pozri odsek nazvanďż˝ Horizontďż˝lne medzery) ďż˝ďż˝rky \thinspace. \dotsm sďż˝ bodky v nďż˝sobnďż˝ch symboloch, napr.

$x_1\times x_2 \times ... \times x_4$

5.4.4. Akcenty v matematickom mďż˝de

\hat a	$\hat a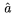$	\check a	$\check a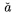$	\tilde a	$\tilde a$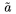
\grave a	$\grave a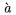$	\dot a	$\dot a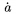$	\ddot a	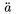$\ddot a$
\ddddot a	$\ddddot a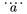$	\breve a	$\breve a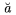$	\bar a	$\bar a$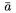
\widehat{xyzuv}	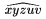$\widehat{xyzuv}$	\widetilde{xyzuv}	$\widetilde{xyzuv}$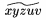
\acute a	$\acute a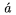$	\dddot a	$\dddot a$	\vec a	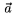$\vec a$

Pozor na rozdiely pri jednoznakovom argumente medzi

$\vec z$

($\vec z $) a

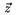
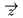
$\overarrow z$

($\overarrow z$) a tieďż˝ medzi

$\bar z$

($\bar z$) a

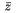
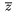
$\overline z$

($\overline z $). Symbol \bar je pouďż˝ďż˝vanďż˝ rovnako ako \B v nematematickom mďż˝de Pozri 3.kapitolu nazvanďż˝ "Nematematickďż˝" mďż˝d. Poslednďż˝ dva akcenty (\widehat, \widetilde) sďż˝ rovnako ďż˝irokďż˝ ako ich argument (najviac vďż˝ak pďż˝ pďż˝smen), pri dlhďż˝om argumente sa umiestďż˝uje nad stred.

\sphat,...,\spvec umiestďż˝ujďż˝ prďż˝sluďż˝nďż˝ akcent na mieste, kde sďż˝ uvedenďż˝, napr. $(I+M)\sptilde$ napďż˝ďż˝e
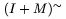
$(I+M)\sptilde$
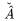
Ak chceme pďż˝saďż˝ nad jednďż˝m znakom dva akcenty, je lepďż˝ie pouďż˝iďż˝ nďż˝zvy akcentov zaďż˝inajďż˝ce s veďż˝kďż˝m pďż˝smenom \Check,...,\Vec. Porovnajte: $\check{\hat A}$ dďż˝va
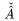
$\check{\hat A}$
zatiaďż˝ ďż˝o $\Check{\Hat A}$ dďż˝va
$\Check{\Hat A}$
ďż˝astďż˝ pouďż˝ďż˝vanie akcentov s veďż˝kďż˝m prvďż˝m pďż˝smenom podstatne predlďż˝uje ďż˝as prekladu, preto je vhodnďż˝ pre ďż˝asto pouďż˝ďż˝vanďż˝ znaky pouďż˝iďż˝ definďż˝ciďż˝ \accentsymbol, napr. \accentsymbol \Ahathat{\Hat}\Hat A}}, ktorďż˝ urďż˝chďż˝jďż˝ preklad. Tďż˝chto definďż˝ciďż˝ by nemalo byďż˝ v dokumente prďż˝liďż˝ veďż˝a (maximďż˝lne 10). Takto vytvorenďż˝ symboly ale nezmenďż˝ujďż˝ automaticky veďż˝kosďż˝, ak ich budeme pouďż˝ďż˝vaďż˝ v exponentoch a indexoch. K vytvoreniu menďż˝ej veďż˝kosti moďż˝no pouďż˝iďż˝ zmenďż˝ovanie pomocou "size". Napr. \accentsymbol\smallAhathat{{\size\Hat{\Hat A}}}

5.4.5. Tuďż˝nďż˝ a inďż˝ matematickďż˝ "textovďż˝" fonty

V matematickom mďż˝de mďż˝me k dispozďż˝cii nasledujďż˝ce "textovďż˝" fonty:

"Blackboard Bold" font --- \Bbb, napr. $\Bbb C, \Bbb R$ dďż˝va
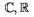
$\Bbb C,\Bbb R$
Pracuje len s veďż˝kďż˝mi pďż˝smenami, okrem $\Bbbk$ , ďż˝o dďż˝va
$\Bbbk$
Pokiaďż˝ pouďż˝ďż˝vame amsppt.sty Pozri 4.kapitolu nazvanďż˝ Moďż˝nosti ďż˝pravy ďż˝lďż˝nku, ktorďż˝ poskytuje "amsppt.sty". sďż˝ tieto fonty nahrďż˝vanďż˝ automaticky, inďż˝ďż˝ musďż˝me napďż˝saďż˝ \loadmsbm na zaďż˝iatok dokumentu.
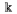
"Gotickďż˝" font --- \frak, napr. $\frak g,\frac G, \frak{jana}$ dďż˝va $\frak g,\frak G,\frak {jana}$. Sďż˝ prďż˝stupnďż˝ malďż˝ i veďż˝kďż˝ pďż˝smenďż˝. Pokiaďż˝ pouďż˝ďż˝vame amsppt.sty sďż˝ tieto fonty nahrďż˝vanďż˝ automaticky, inďż˝ďż˝ musďż˝me napďż˝saďż˝ \loadeufm na zaďż˝iatok dokumentu.
"Kaligrafickďż˝" font --- \Cal, napr. $\Cal A, \Cal B$ dďż˝va
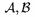
$\Cal A,\Cal B$
Pracuje len s veďż˝kďż˝mi pďż˝smenami.
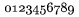
"Starďż˝ ďż˝ďż˝slicovďż˝" font --- \oldnos, prďż˝stupnďż˝ len pre ďż˝ďż˝slice 0 aďż˝ 9; napr. $\oldnos{0123456789}$ dďż˝va
$\oldnos{0123456789}$

Ak chceme pouďż˝ďż˝vaďż˝ tuďż˝nďż˝ znaky v matematickom mďż˝de, musďż˝me napďż˝saďż˝ \loadbold v preambulovej ďż˝asti dokumentu, ďż˝ďż˝m sa nďż˝m nahrajďż˝ tuďż˝nďż˝ fonty matematickej kurzďż˝vy, grďż˝ckych pďż˝smen (cmmib) a zďż˝kladnďż˝ch matematickďż˝ch symbolov (cmbsy).

\bold je aplikovateďż˝nďż˝ na vďż˝etky pďż˝smena a ďż˝ďż˝sla, napďż˝ďż˝e nasledujďż˝ce pďż˝smeno tuďż˝nďż˝m romďż˝nskym fontom, ak chceme aplikovaďż˝ na viac pďż˝smen, nutnďż˝ daďż˝ do {...}, napr.$\bold A,\bold{Pr1}$ dďż˝va
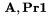
$\bold A,\bold{Pr1}$
\boldkey je aplikovateďż˝nďż˝ na vďż˝etky klďż˝vesnicovďż˝ znaky, znaky tlaďż˝ďż˝ tuďż˝nou matematickou kurzďż˝vou, napr. $\boldkey a\boldkey b\boldkey +\boldkey=\boldkey!$ dďż˝va
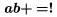
$\loadbold$\boldkey a\boldkey b\boldkey +\boldkey =\boldkey !$$
\boldsymbol sa dďż˝ aplikovaďż˝:
--- na malďż˝ i veďż˝kďż˝ grďż˝cke pďż˝smena, napr. $\boldsymbol\omega, \boldsymbol\Omega, \boldsymbol\varOmega$ dďż˝va po rade
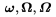
$\loadbold$\boldsymbol\omega, \boldsymbol\Omega, \boldsymbol\varOmega$$

--- na vďż˝etky ostatnďż˝ ďż˝tandardnďż˝ symboly, ktorďż˝ sďż˝ ďż˝pecifikovanďż˝ jednoduchďż˝m kontrolslovom, napr. $\boldsymbol A^{\boldsymbol\prime}$ dďż˝va
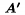
$\loadbold$\boldsymbol A^{\boldsymbol\prime}$$
(Ale kratďż˝ia forma \prime tvaru ' nepracuje.)
--- na zďż˝tvorky a oddeďż˝ovaďż˝e, napr. $\boldsymbol\{\dots\boldsymbol\},\boldsymbol\vert, \boldkey|$ dďż˝va
$\loadbold$\boldsymbol\{...\boldsymbol\}, \boldsymbol\vert, \boldkey|$$

--- \boldsymbol nemďż˝ďż˝eme pouďż˝iďż˝ po \left a \right.
Prďż˝stupnďż˝ sďż˝ napr.\ aj tuďż˝nďż˝ kaligrafickďż˝ pďż˝smenďż˝ a starďż˝ (oldnos) ďż˝ďż˝slovky, avďż˝ak tieto sa musia pďż˝saďż˝ cez kďż˝dy prďż˝sluďż˝nďż˝ch znakov odpovedajďż˝ce ich umiestneniu v tabuďż˝ke prďż˝sluďż˝nďż˝ho fontu. Napr. \font\boldznak = cmsy10{\boldznak\char65} dďż˝va tuďż˝nďż˝ kaligrafickďż˝
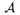
${\font\boldznak=cmsy10 \boldznak \char65}$
Ak potrebujeme v matematickom mďż˝de napďż˝saďż˝ tuďż˝ne len 1--2 symboly, mďż˝ďż˝eme pouďż˝iďż˝ \pmb, ďż˝o je sďż˝ce "horďż˝ia" tuďż˝nďż˝ kvalita tďż˝chto znakov, ale uďż˝etrďż˝me pamďż˝, pretoďż˝e nepotrebujeme naďż˝ďż˝taďż˝ tuďż˝nďż˝ fonty. Napr. $\pmb+$ dďż˝va
$\pmb+$
(Okrem toho v matematickom mďż˝de mďż˝ďż˝eme maďż˝ naďż˝ďż˝tanďż˝ch najviac 16 fontov.)

5.4.6. Horizontďż˝lne medzery

\, alebo \thinspace znamenďż˝ ďż˝zku medzeru ďż˝ďż˝rky
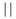
$\vert\, \vert$
Pouďż˝ďż˝va sa v matematickom mďż˝de napr. za vďż˝kriďż˝nďż˝kom (v zmysle faktoriďż˝lu), za ktorďż˝m nasleduje pďż˝smeno, ďż˝ďż˝slica alebo zďż˝tvorky; za odmocninou, aby ďż˝alďż˝ďż˝ text nebol tesne za odmocninou; medzi dx, dy pri integrďż˝loch.
\! alebo \negthinspace je zďż˝pornďż˝ medzera ďż˝ďż˝rky medzery \,.
@. je asi 1/10 z \, analogicky @! pre rovnako veďż˝kďż˝ zďż˝pornďż˝ medzeru.
\medspace je kladnďż˝ medzera ďż˝ďż˝rky
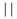
$\vert\medspace\vert$
a odpovedďż˝ veďż˝kosti medzery, ktorďż˝ TeX vkladďż˝ okolo binďż˝rnych operďż˝torov (\negmedspace) analogickďż˝ zďż˝pornďż˝ medzera).
\thickspace je kladnďż˝ medzera ďż˝ďż˝rky
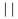
$\vert\thickspace\vert$
a odpovedďż˝ veďż˝kosti medzery, ktorďż˝ TeX vkladďż˝ okolo binďż˝rnych relďż˝ciďż˝ (\negthickspace analogickďż˝ zďż˝pornďż˝ medzera).
\quad je medzera ďż˝irokďż˝ asi ako 2 normďż˝lne ďż˝ďż˝rky
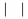
$\vert\quad\vert$
\qquad je skratka za \quad \quad. Spravidla vedďż˝ajďż˝ia podmienka bďż˝va vzdialenďż˝ o \qquad, napr. $F_n=F_{n+1}+F_{n+2},\qquad n>1$ dďż˝va
$F_n=F_{n+1}+F_{n+2},\qquad n>1$
\hskip,\kern, \hphantom,\phantom popis ktorďż˝ch je uvedenďż˝ v textovom mďż˝de Pozri 3.kapitolu nazvanďż˝ "Nematematickďż˝" mďż˝d.

5.4.7. Vertikďż˝lne medzery

V ktorejkoďż˝vek matematickej konďż˝trukcii pouďż˝ďż˝vajďż˝cej \\ (viac centrovanďż˝ch formuliek pďż˝sanďż˝ch pod sebou v rďż˝mci nejakďż˝ho okolia v $$...$$, centrovanďż˝ formulky (Pozri odsek nazvanďż˝ ďż˝ďż˝slovanie a ďż˝prava centrovanďż˝ch formuliek) je moďż˝nďż˝ pďż˝saďż˝ za \\ \vspace {<vzd>} a prďż˝sluďż˝ne vysokďż˝ riadok bude vynechanďż˝.
Ak v centrovanej formulke hneďż˝ za $$ napďż˝ďż˝eme \spreadlines{<vzd>}, bude sa uvedenďż˝ vzdialenosďż˝ vkladaďż˝ za kaďż˝dďż˝m riadkom oddelenďż˝m \\. (Nevzďż˝ahuje sa na matice, kde rovnakďż˝ efekt mďż˝ slovo \spreadlinematrixs, ktorďż˝ tieďż˝ funguje pri \cases).
\smash{...} -- pokiaďż˝ obsah zďż˝tvorky presahuje nad, ďż˝i pod riadok, nemďż˝ to vplyv na zvďż˝ďż˝enie medzery medzi riadkami. Analogicky \topsmash a \botsmash bude ignorovaďż˝ presah nad, ďż˝i pod riadkom. Napr. $\botsmash{\dfrac 12}$ spďż˝sobďż˝ neodsadenie riadku v ktorom sa vďż˝raz vyskytol.
\vskip, \vglue, \kern, \hphantom popis ktorďż˝ch je uvedenďż˝ v textovom mďż˝de.

Spďż˝	Obsah	ďż˝alej
TeXovďż˝ matematickďż˝ vďż˝razovďż˝ prostriedky	Hore	ďż˝ďż˝slovanie a ďż˝prava centrovanďż˝ch formuliek